Imports
Loading required package: xts
Loading required package: zoo
The following objects are masked from 'package:base':
as.Date, as.Date.numeric
Loading required package: TTR
Registered S3 method overwritten by 'quantmod':
method from
as.zoo.data.frame zoo
library (ggplot2)library (purrr) # partial function library (glue) # string interpolation
RNGkind (sample.kind= "Rounding" )
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
GetData
When you click the Render button a document will be generated that includes both content and the output of embedded code. You can embed code like this:
<- function (s, date_filter= "1979-12-31/2017-12-31" , new_name= 'TR' ){<- na.omit (s); s<- s[date_filter]; snames (s) <- new_name; sreturn (s)<- function (name, date_filter= "1979-12-31/2017-12-31" , src= 'FRED' , new_name= 'TR' ){<- getSymbols (name, src= src, auto.assign = FALSE ); s<- filterSeries (s)return (s)getSeries ("WILL5000IND" ) |> head (n= 3 )
TR
1979-12-31 1.90
1980-01-02 1.86
1980-01-04 1.88
Utility functions
<- function (tbl){<- data.frame (date= index (tbl), TR= as.numeric (tbl$ TR))return (df)getSeries ("WILL5000IND" ) |> head (n= 3 ) |> get_df ()
1979-12-31 1.90 1980-01-02 1.86 1980-01-04 1.88
<- function (tbl){return (diff (log (tbl))[- 1 ])<- function (tbl, fn){<- fn (tbl, sum)return (result)<- partial (aggr_fn, fn = apply.weekly)<- partial (aggr_fn, fn = apply.monthly)<- partial (aggr_fn, fn = apply.quarterly)<- partial (aggr_fn, fn = apply.yearly)<- function (logret){return (exp (logret)- 1 )
Visualization
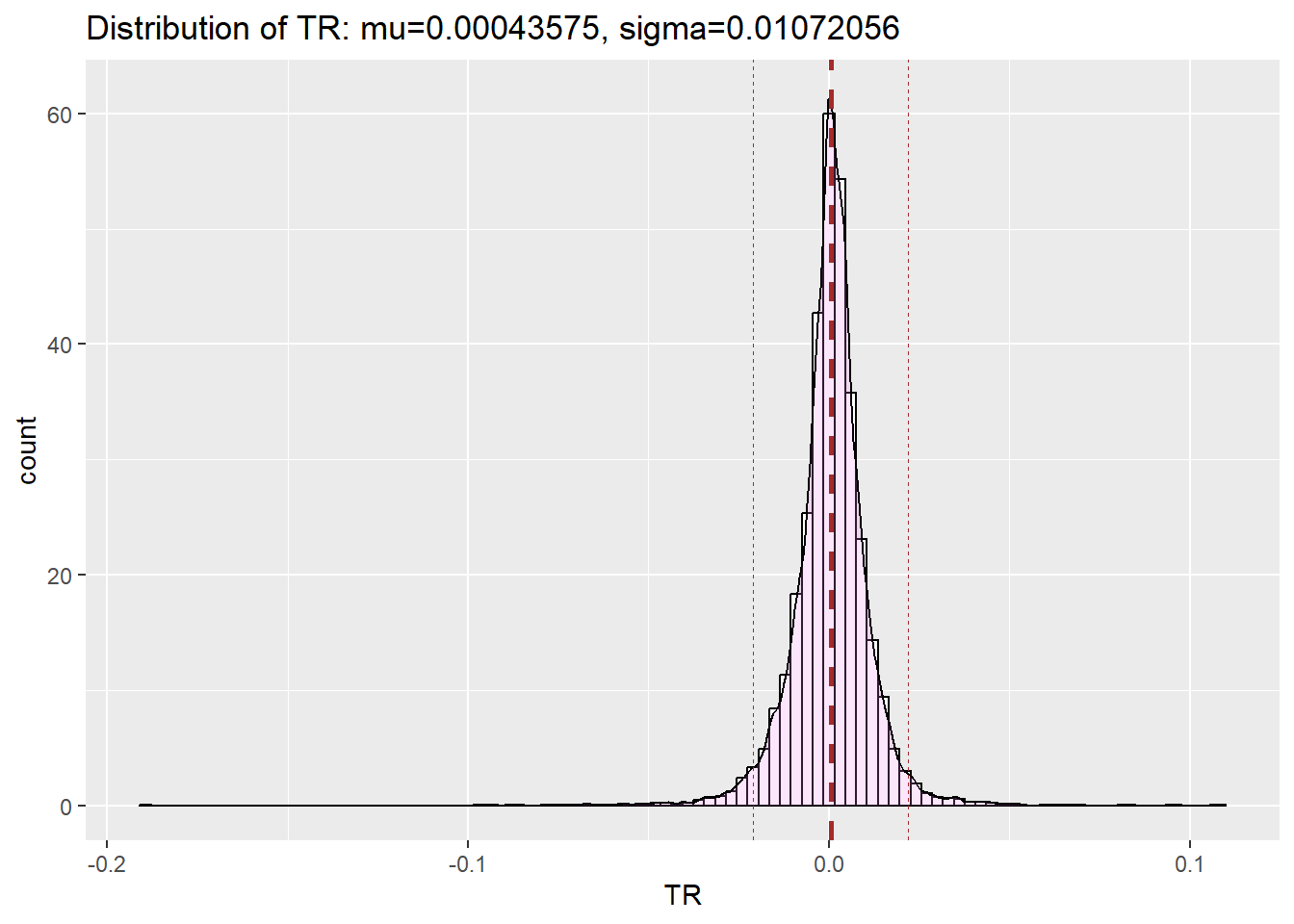
<- function (tbl){= mean (tbl)= sd (tbl)<- get_df (tbl) |> ggplot (mapping = aes (x= TR)) + geom_histogram (aes (y= after_stat (density)), colour= "black" , fill= "white" , bins= 100 )+ geom_density (alpha= .2 , fill= "violet" ) + geom_vline (aes (xintercept= mu),color= "brown" , linetype= "dashed" , linewidth= 1 ) + geom_vline (aes (xintercept= mu+ 2 * sig),color= "brown" , linetype= "dashed" , linewidth= 0.1 ) + geom_vline (aes (xintercept= mu-2 * sig),color= "brown" , linetype= "dashed" , linewidth= 0.1 ) + labs (title= glue ("Distribution of TR: mu={round(mu, 8)}, sigma={round(sig, 8)}" ), y= 'count' )return (p)
<- getSeries ("WILL5000IND" )|> logret_1 () |> get_dist_plot ()
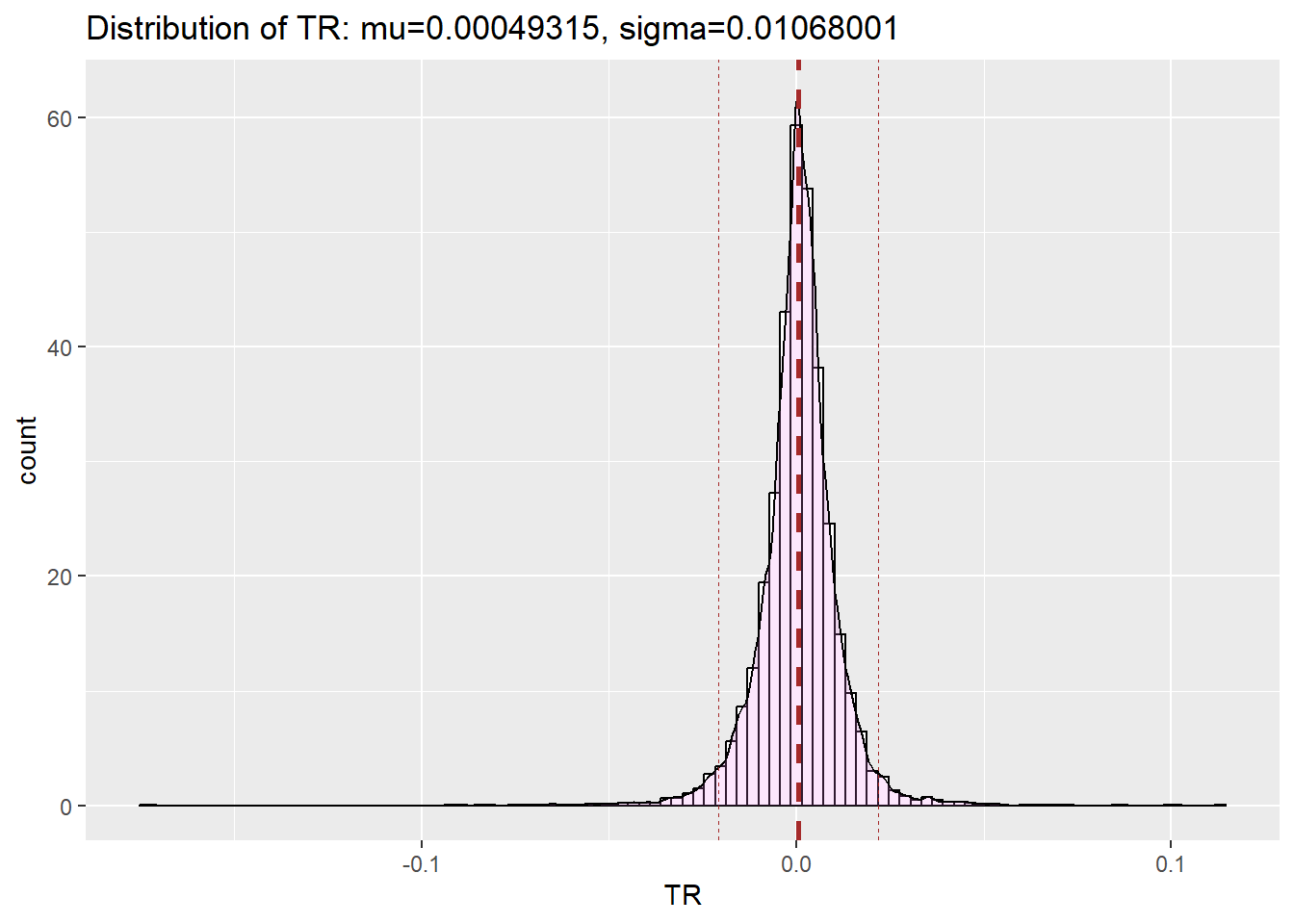
|> logret_1 () |> ret () |> get_dist_plot ()
Exercise 5
load ("W1_Exercise2_FRED_gold.gz" ); gold
TR
1980-01-02 559.50
1980-01-03 634.00
1980-01-04 588.00
1980-01-07 633.50
1980-01-08 610.00
1980-01-09 607.20
1980-01-10 602.85
1980-01-11 623.00
1980-01-14 660.00
1980-01-15 684.00
...
2017-12-12 1240.90
2017-12-13 1242.65
2017-12-14 1251.00
2017-12-15 1254.60
2017-12-18 1260.60
2017-12-19 1260.35
2017-12-20 1264.55
2017-12-21 1264.55
2017-12-27 1279.40
2017-12-28 1291.00
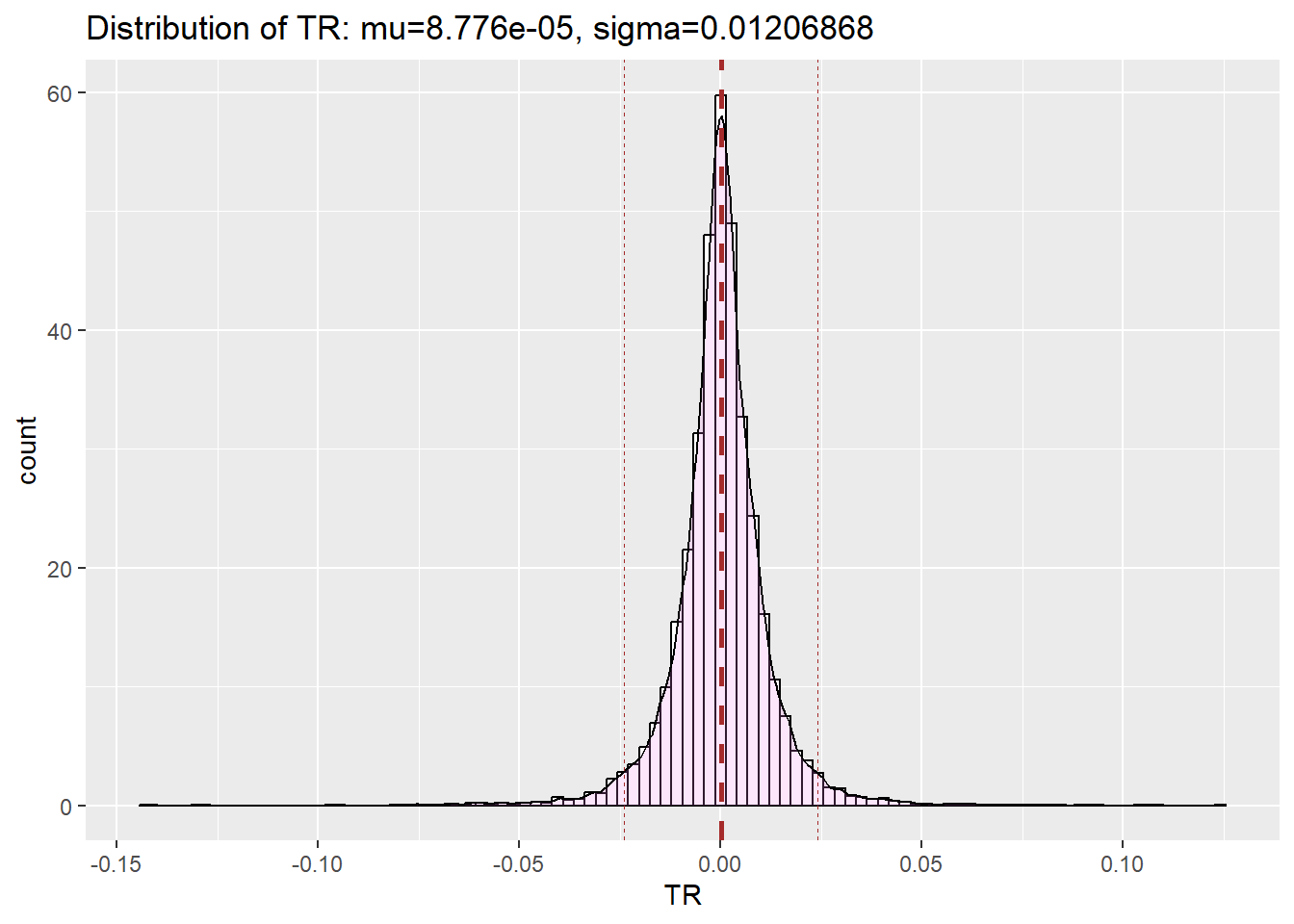
|> filterSeries () |> logret_1 () |> get_dist_plot ()
Value-at-Risk(VaR)
VaR: the amount that a portfolio might lose, with a given probability (1-𝛼), over a given time period.
𝛼 is typically 0.10, 0.05, or 0.01
The time period is typically 1 day or 1 week
𝛼 quantile of probability density function
Example: 𝛼 = 0.05; time period = 1 day. What is the 1-day VaR at the 95% confidence level of the portfolio?
Here, the VaR is the maximum loss in the portfolio, over the next trading day, if we exclude the worst 5% of possible outcomes.
<- function (tbl,alpha= 0.05 ){= mean (tbl)= sd (tbl)= qnorm (alpha, mean= mu, sd= sig) #quantile of normal distribution(only not for any other distribution) return (VaR)<- function (portfolio, risk_num){ #95% confidence that we won't loose more than this amount return (portfolio* (exp (risk_num)- 1 ))|> logret_1 () |> get_VaR () |> round (digits= 6 )
<- wilsh |> logret_1 () |> get_VaR (); wilsh_VaRexpected_loss (1000 , wilsh_VaR)
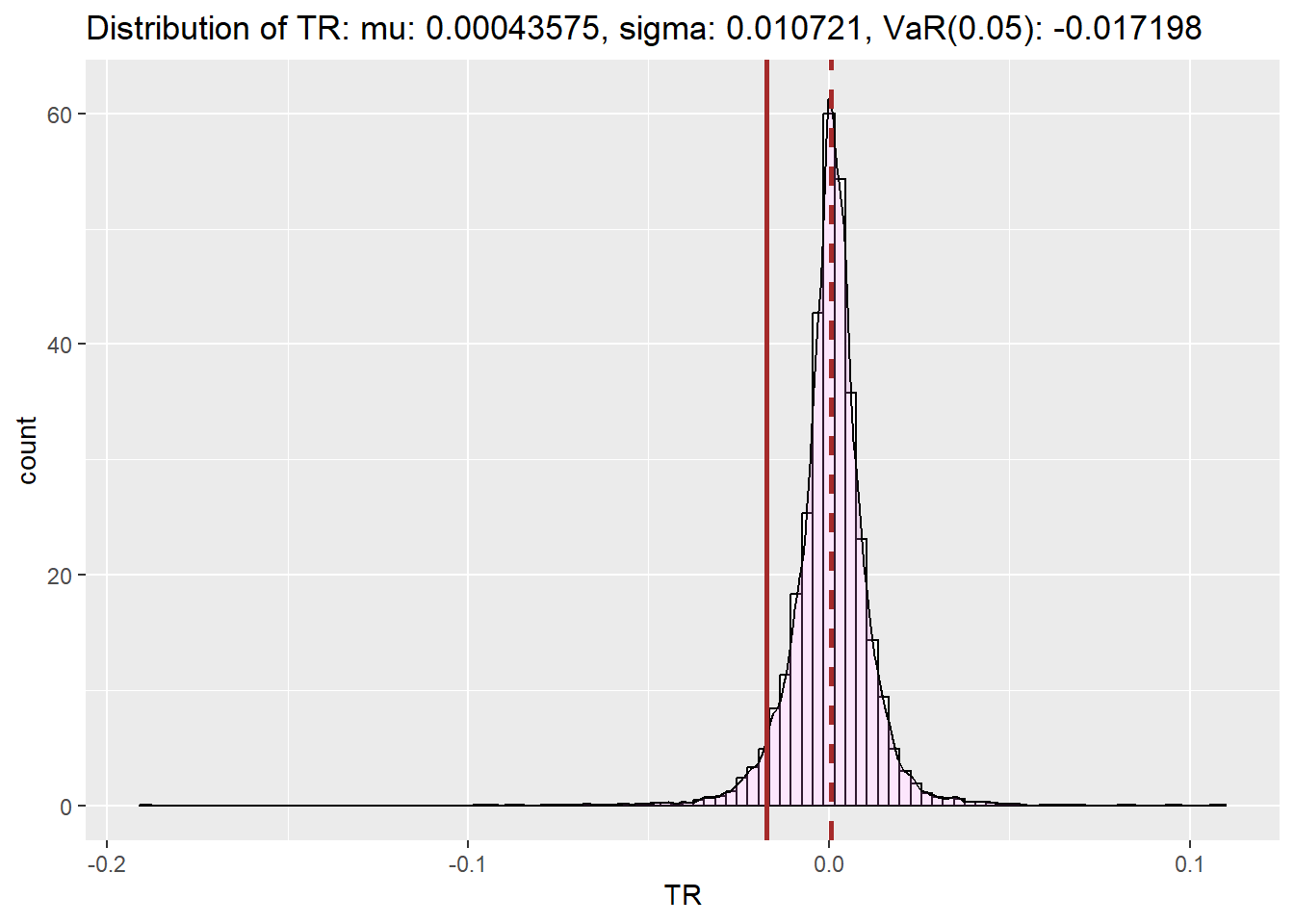
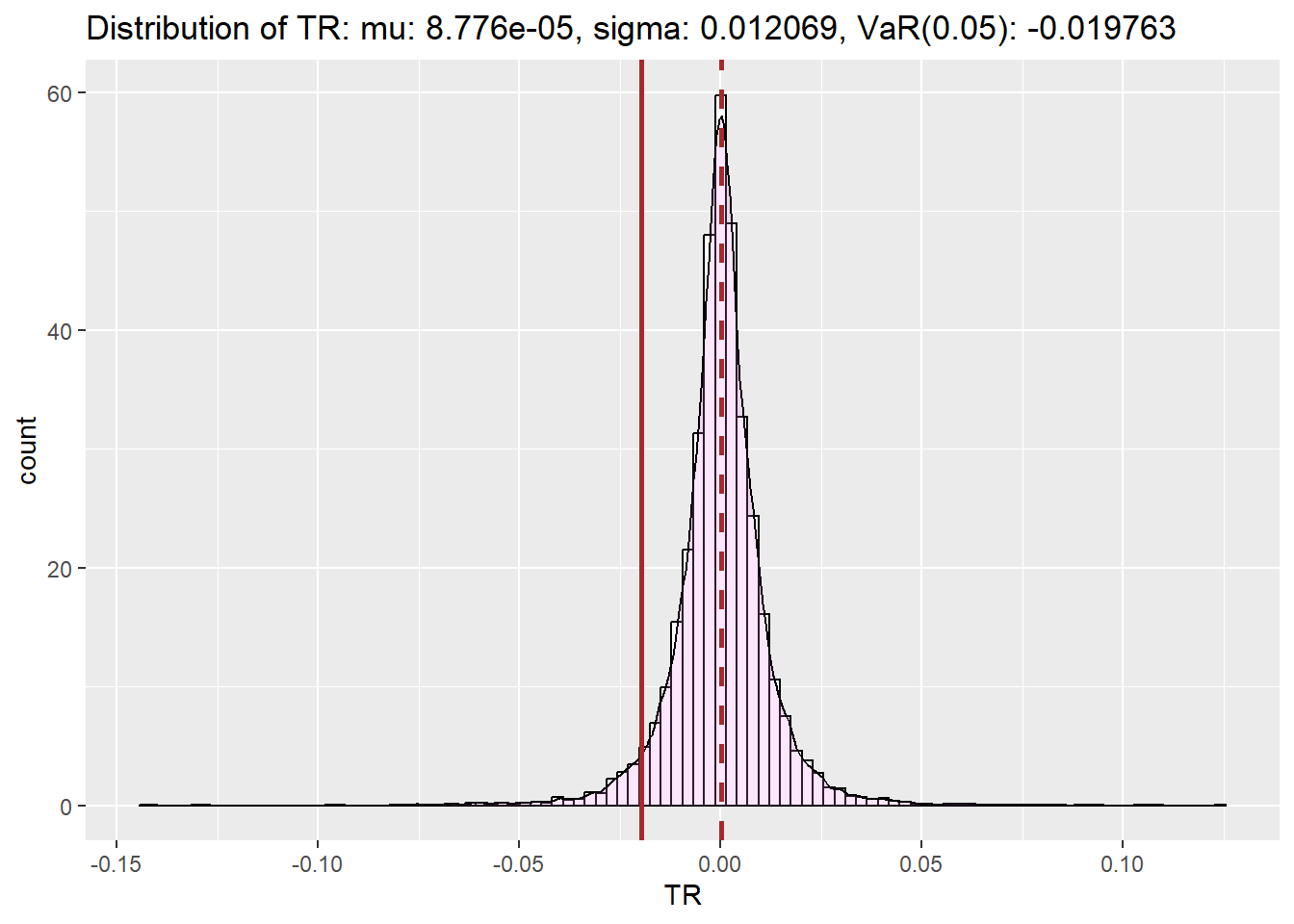
<- function (tbl, alpha= 0.05 ){= mean (tbl)= sd (tbl)= qnorm (alpha, mean= mu, sd= sig)<- get_df (tbl) |> ggplot (mapping = aes (x= TR)) + geom_histogram (aes (y= after_stat (density)), colour= "black" , fill= "white" , bins= 100 )+ geom_density (alpha= .2 , fill= "violet" ) + geom_vline (aes (xintercept= mu),color= "brown" , linetype= "dashed" , linewidth= 1 ) + geom_vline (aes (xintercept= VaR),color= "brown" , linewidth= 1 ) + labs (title= glue ("Distribution of TR: mu: {round(mu, 8)}, sigma: {round(sig, 6)}, VaR({alpha}): {round(VaR, 6)}" ), y= 'count' )return (p)|> logret_1 () |> get_VaR_plot ()
Exercise 6
load ("D:/rahuketu/PPV/S_Self_Study/FinancialRiskManagementR/W1_Exercise2_FRED_gold.gz" )head (gold)
TR
1980-01-02 559.5
1980-01-03 634.0
1980-01-04 588.0
1980-01-07 633.5
1980-01-08 610.0
1980-01-09 607.2
|> filterSeries () |> logret_1 () |> get_VaR_plot ()
<- gold |> logret_1 () |> get_VaR () |> round (digits= 6 ); gold_VaRexpected_loss (1000 , gold_VaR) |> round (digits= 1 )
Expected Shortfall (ES)
Other names
Definition: For the same values of 1 − α 1 - \alpha
In our simple example, a hedge fund has $100 million of investor capital, borrows another $900 million from a bank, and invests the combined $1 billion into the Wilshire 5000 index.
What does the 1-day 95% ES tell us?
Answer: Over 1 day, if US equities fell by more than the VaR, the hedge fund is expected to lose $21.4 million:
$1000 million × [ exp(ES) – 1 ]
<- function (tbl, alpha= 0.05 ){= mean (tbl)= sd (tbl)= mu - sig* dnorm (qnorm (alpha, mean= 0 , sd= 1 ), 0 , 1 )/ alpha #quantile of normal distribution(only not for any other distribution) return (ES)<- wilsh |> logret_1 () |> get_ES () |> round (digits= 6 ); wilsh_ESexpected_loss (1000 , wilsh_ES)
Exercise 7
<- gold |> logret_1 () |> get_ES () |> round (digits= 6 ); gold_ESexpected_loss (1000 , gold_ES) |> round (digits= 1 )
Simulation to Estimate VaR and ES
# get_norm_tbl <- function(mu, sig, n=100000){ # s <- rnor # } = 10 = 0 = 1 rnorm (n,mu, sig)
[1] -0.77986007 0.14633315 1.84487164 0.81671406 -0.76264749 -0.09190092
[7] -0.86716597 0.96884444 0.64690758 0.42256862
<- function (mu, sig, n= 100000 ){RNGkind (sample.kind= "Rounding" )set.seed (123789 )return (rnorm (n,mu, sig)) get_norm_series (mu, sig) |> head ()
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
[1] -0.77986007 0.14633315 1.84487164 0.81671406 -0.76264749 -0.09190092
<- function (s, n= 100000 ){RNGkind (sample.kind= "Rounding" )set.seed (123789 )return (sample (as.vector (s), n, replace= TRUE ))get_sim_series (data.frame (a = 1 : 3 )$ a, n= 10 )
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- function (s, alpha= 0.05 ){return (quantile (s, alpha) |> unname ())<- get_norm_series (0 , 1 )
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- s |> get_sim_VaR (); VaR
<- function (s, VaR){# VaR <- get_sim_VaR(s, alpha=alpha) return (mean (s[s< VaR]))|> get_sim_ES (VaR= VaR)
<- function (a, b){return ((a- b)/ a* 100 )<- s |> get_VaR ()<- s |> get_sim_VaR ()err (a, b)|> round (digits = 2 )
<- wilsh |> logret_1 ()<- s |> get_VaR (); VaR<- s |> get_sim_series ()
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- s_sim|> get_sim_VaR (); VaR_sim<- s_sim |> get_sim_ES (VaR= VaR_sim); ES_simerr (VaR, VaR_sim) |> round (digits = 2 )err (ES, ES_sim) |> round (digits = 2 )
<- wilsh |> logret_1 ()<- mean (s)<- sd (s)<- get_norm_series (mu, sig)
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- s |> get_sim_series ()
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- norm_s |> get_sim_VaR (); VaR<- norm_s |> get_sim_ES (VaR= VaR); ES<- s_sim|> get_sim_VaR (); VaR_sim<- s_sim |> get_sim_ES (VaR= VaR_sim); ES_simerr (VaR, VaR_sim) |> round (digits = 2 )err (ES, ES_sim) |> round (digits = 2 )
data.frame (TR= s_sim) |> head ()
1 0.008019289 2 0.010661866 3 -0.004821868 4 0.001630752 5 0.004629400 6 0.006427711
<- wilsh |> logret_1 ()<- mean (s)<- sd (s)<- get_norm_series (mu, sig)
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
data.frame (TR= norm_s) |> head ()
1 -0.0079247909 2 0.0020045205 3 0.0202138069 4 0.0091913802 5 -0.0077402624 6 -0.0005494825
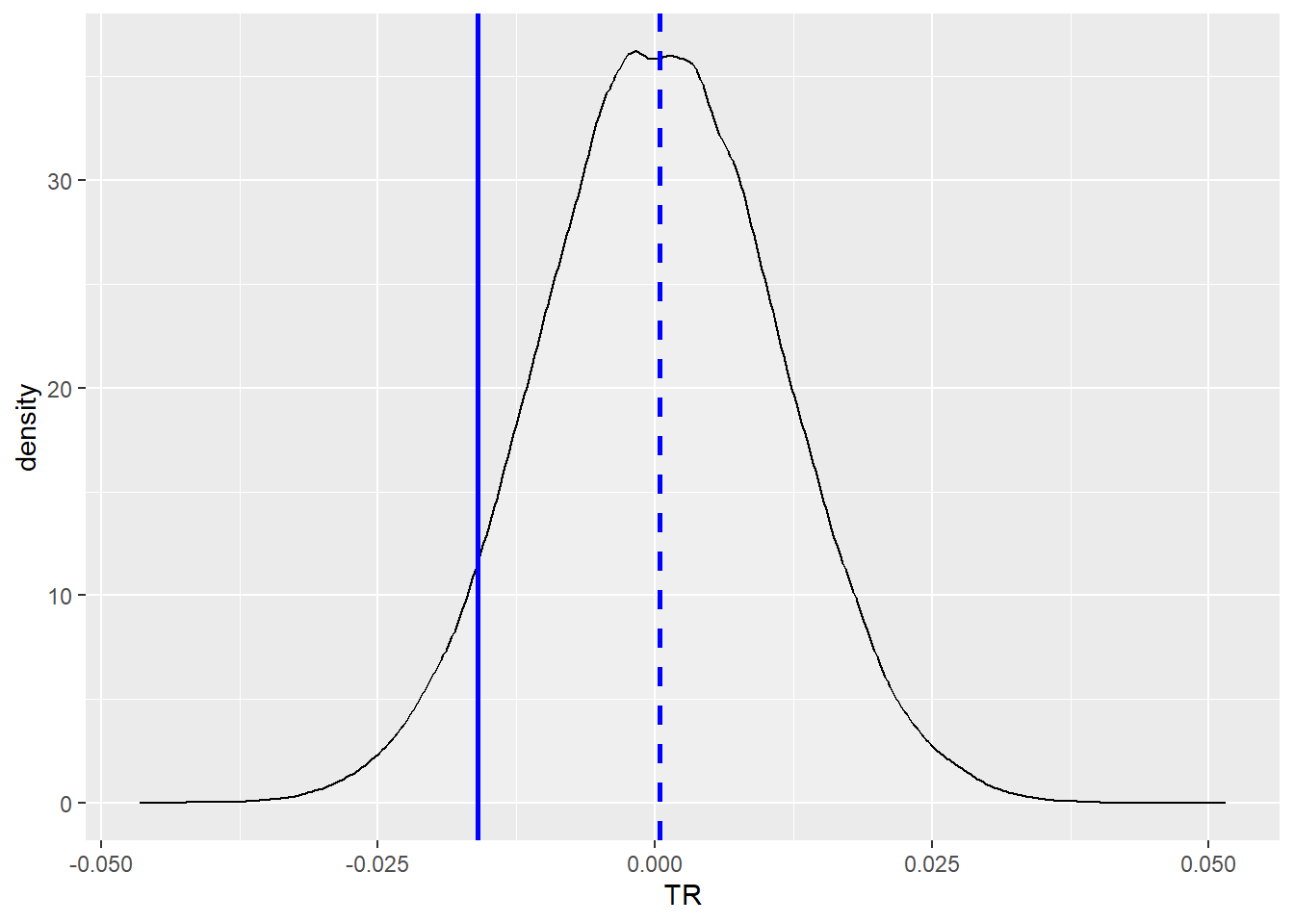
<- data.frame (TR= norm_s) |> ggplot (mapping = aes (x= TR)) + geom_density (alpha= .2 , fill= "white" ) + geom_vline (aes (xintercept= mu),color= "blue" , linetype= "dashed" , linewidth= 1 ) + geom_vline (aes (xintercept= VaR_sim),color= "blue" , linewidth= 1 )
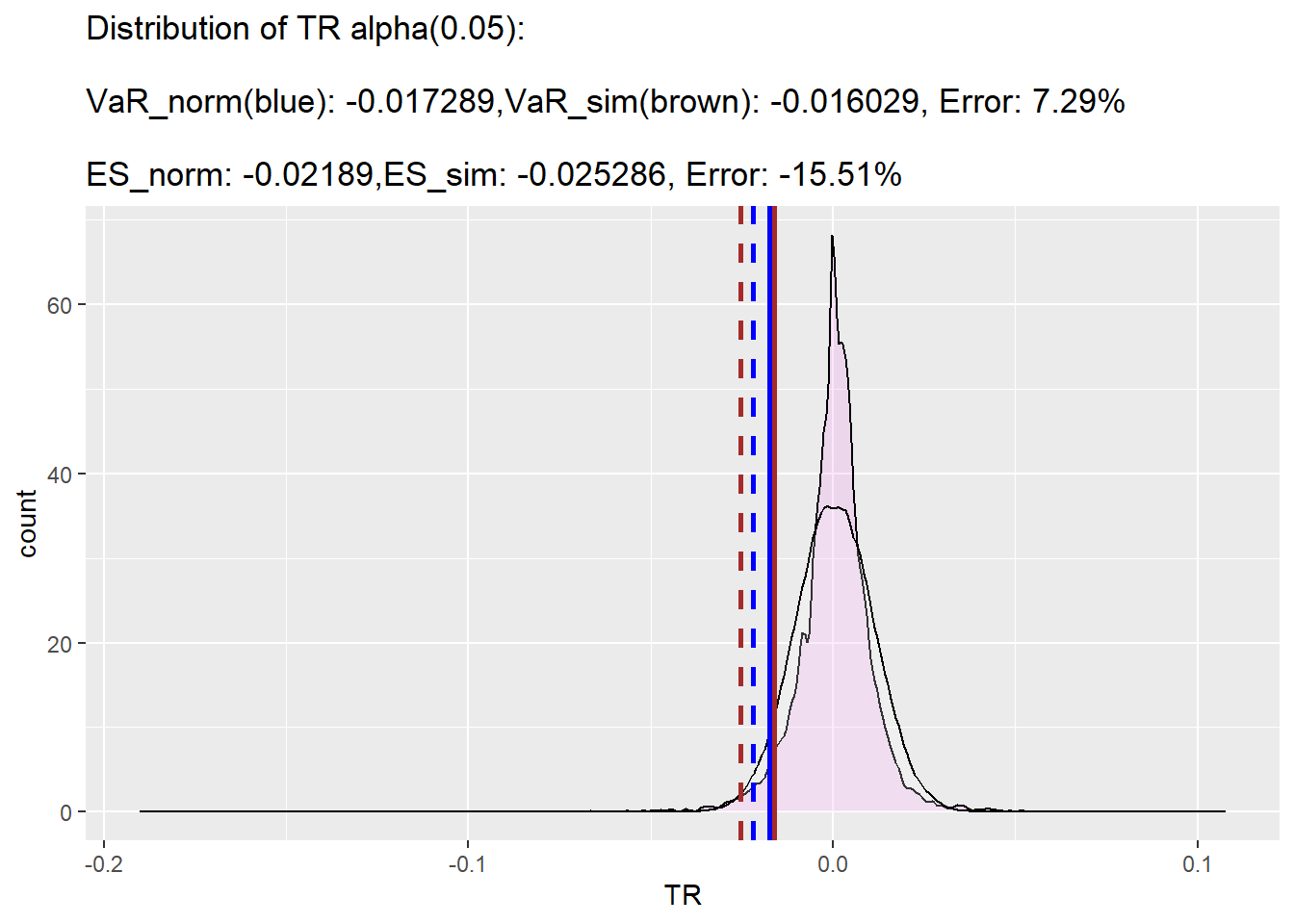
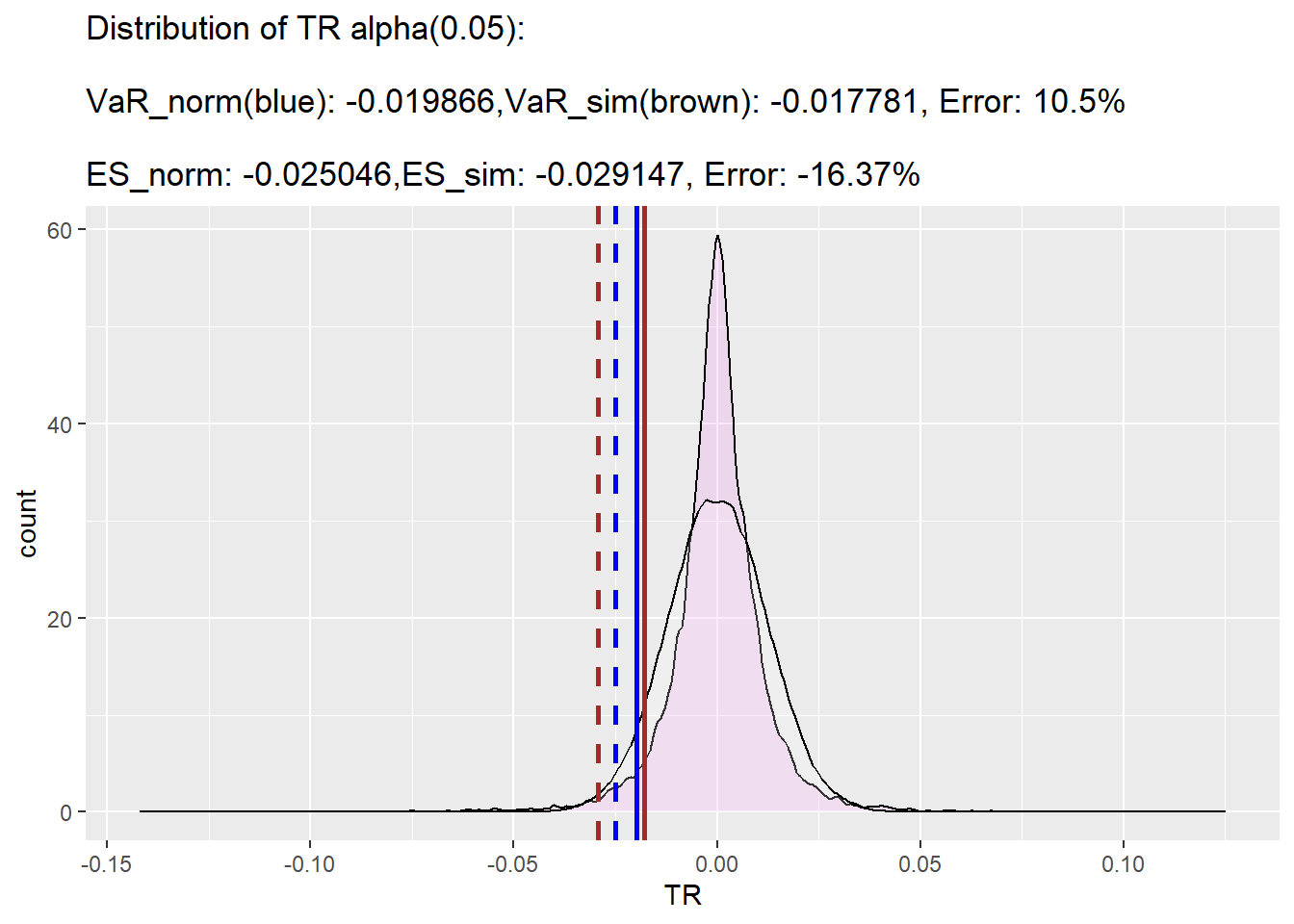
<- function (s, alpha= 0.05 ){<- mean (s)<- sd (s)<- get_norm_series (mu, sig)<- norm_s |> get_sim_VaR (); VaR<- norm_s |> get_sim_ES (VaR= VaR); ES<- s |> get_sim_series ()<- s_sim|> get_sim_VaR (); VaR_sim<- s_sim |> get_sim_ES (VaR= VaR_sim); ES_sim<- err (VaR, VaR_sim) |> round (digits = 2 )<- err (ES, ES_sim) |> round (digits = 2 )<- data.frame (TR= s_sim, TR2= norm_s) |> ggplot () + geom_density (mapping = aes (x= TR), alpha= .2 , fill= "violet" ) + geom_density (mapping = aes (x= TR2), alpha= .2 , fill= "white" ) + geom_vline (aes (xintercept= ES_sim),color= "brown" , linetype= "dashed" , linewidth= 1 ) + geom_vline (aes (xintercept= ES),color= "blue" , linetype= "dashed" , linewidth= 1 ) + geom_vline (aes (xintercept= VaR_sim),color= "brown" , linewidth= 1 ) + geom_vline (aes (xintercept= VaR),color= "blue" , linewidth= 1 ) + labs (title= glue ("Distribution of TR alpha({alpha}): \n VaR_norm(blue): {round(VaR, 6)},VaR_sim(brown): {round(VaR_sim, 6)}, Error: {round(err(VaR, VaR_sim), 2)}% \n ES_norm: {round(ES, 6)},ES_sim: {round(ES_sim, 6)}, Error: {round(err(ES, ES_sim), 2)}%" ), y= 'count' )return (p)|> logret_1 () |> get_comp_plot ()
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
Exercise 8
|> filterSeries () |> logret_1 () |> get_comp_plot ()
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
set.seed (123789 )<- gold |> filterSeries () |> logret_1 ()<- mean (s)<- sd (s)<- get_norm_series (mu, sig)
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- s |> get_sim_series ()
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- norm_s |> get_sim_VaR (); VaR |> round (digits= 6 )<- norm_s |> get_sim_ES (VaR= VaR); ES |> round (digits= 6 )<- s_sim|> get_sim_VaR (); VaR_sim |> round (digits= 6 )<- s_sim |> get_sim_ES (VaR= VaR_sim); ES_sim |> round (digits= 6 )err (VaR, VaR_sim) |> round (digits = 2 )err (ES, ES_sim) |> round (digits = 2 )
Quiz 1
<- getSymbols ("DEXJPUS" , src= 'FRED' , auto.assign = FALSE )<- na.omit (us2yen)<- us2yen["1979-12-31/2017-12-31" ]<- 1 / us2yen; yen2us |> head ()
DEXJPUS
1979-12-31 0.004161465
1980-01-02 0.004193751
1980-01-03 0.004195511
1980-01-04 0.004258944
1980-01-07 0.004318722
1980-01-08 0.004259851
set.seed (123789 )<- yen2us |> logret_1 ()<- mean (s); mu |> round (digits= 6 )<- sd (s); sig |> round (digits= 6 )<- get_norm_series (mu, sig)
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- s |> get_sim_series ()
Warning in RNGkind(sample.kind = "Rounding"): non-uniform 'Rounding' sampler
used
<- s |> get_VaR (alpha= 0.01 ); VaR |> round (digits= 6 )<- s |> get_ES (alpha= 0.01 ); ES |> round (digits= 6 )<- norm_s |> get_sim_VaR (alpha= 0.01 ); VaR_norm |> round (digits= 6 )<- norm_s |> get_sim_ES (VaR= VaR_norm); ES_norm |> round (digits= 6 )<- s_sim|> get_sim_VaR (alpha= 0.01 ); VaR_sim |> round (digits= 6 )<- s_sim |> get_sim_ES (VaR= VaR_sim); ES_sim |> round (digits= 6 )err (VaR_norm, VaR_sim) |> round (digits = 2 )err (ES_norm, ES_sim) |> round (digits = 2 )
expected_loss (1000 , ES_sim) |> round (digits= 2 )