Signal Processing using Octave

Preliminary Setup

pkg load signal

graphics_toolkit("notebook")

Read the Data

load(fullfile(cd, "resources","section_01","glassDance.mat" )); whos

Variables visible from the current scope:

variables in scope: top scope

  Attr   Name           Size                     Bytes  Class
  ====   ====           ====                     =====  ===== 
         ans            1x1                          1  logical
         doc_file       1x84                        84  char
         glassclip 661500x2                   10584000  double
         pkg_dir        1x69                        69  char
         srate          1x1                          8  double

Total is 1323155 elements using 10584162 bytes

help soundsc

'soundsc' is a function from the file /opt/homebrew/Caskroom/miniforge/base/envs/octave/share/octave/7.3.0/m/audio/soundsc.m

 -- soundsc (Y)
 -- soundsc (Y, FS)
 -- soundsc (Y, FS, NBITS)
 -- soundsc (..., [YMIN, YMAX])
     Scale the audio data Y and play it at sample rate FS to the default
     audio device.

     The audio signal Y can be a vector or a two-column array,
     representing mono or stereo audio, respectively.

     If FS is not given, a default sample rate of 8000 samples per
     second is used.

     The optional argument NBITS specifies the bit depth to play to the
     audio device and defaults to 8 bits.

     By default, Y is automatically normalized to the range [-1, 1].  If
     the range [YMIN, YMAX] is given, then elements of Y that fall
     within the range YMIN ≤ Y ≤ YMAX are scaled to the range [-1, 1]
     instead.

     For more control over audio playback, use the ‘audioplayer’ class.

     See also: sound, record.

Additional help for built-in functions and operators is
available in the online version of the manual.  Use the command
'doc <topic>' to search the manual index.

Help and information about Octave is also available on the WWW
at https://www.octave.org and via the help@octave.org
mailing list.

pnts = length(glassclip)

pnts = 661500

timevec = (0:pnts-1)/srate;whos

Variables visible from the current scope:

variables in scope: top scope

  Attr   Name           Size                     Bytes  Class
  ====   ====           ====                     =====  ===== 
         ans            1x1                          8  double
         doc_file       1x84                        84  char
         glassclip 661500x2                   10584000  double
         pkg_dir        1x69                        69  char
         pnts           1x1                          8  double
         srate          1x1                          8  double
         timevec        1x661500               5292000  double

Total is 1984656 elements using 15876177 bytes

Time Domain Signal

figure(1), clf
subplot(1,2, 1:2)
plot(timevec, glassclip)
xlabel('Time (s) ')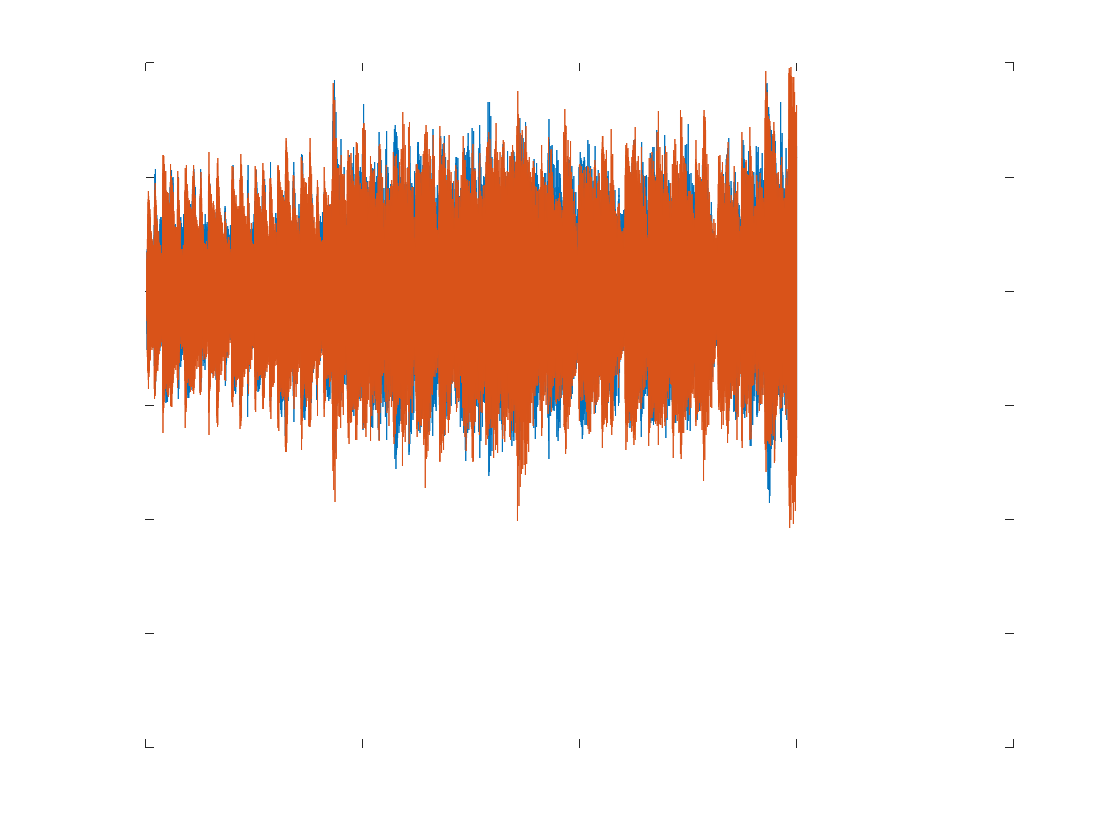

warning: opengl_renderer::render_text: support for rendering text (FreeType) was unavailable or disabled when Octave was built
warning: called from
    axes at line 107 column 8
    subplot at line 335 column 18

warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)

Plot shows a lot of narrow band activity

Power Spectrum

linspace(0,1,5)

ans	1	2	3	4	5
1	0	0.25	0.5	0.75	1

For calculating points 1. We set range between 0 to sampling_rate/2(Nyquist?) 2. We split this range in floor(length(signal)/2)+1 points. Why? 3. We calculate power spectrum for a single channel

channel = 1 # Will be between 1 and 2

channel = 1

floor(length(glassclip)/2) +1

ans = 330751

hz = linspace(0, srate/2, floor(length(glassclip)/2) +1); whos

Variables visible from the current scope:

variables in scope: top scope

  Attr   Name           Size                     Bytes  Class
  ====   ====           ====                     =====  ===== 
         ans            1x1                          8  double
         channel        1x1                          8  double
         doc_file       1x84                        84  char
         glassclip 661500x2                   10584000  double
         hz             1x330751               2646008  double
         pkg_dir        1x69                        69  char
         pnts           1x1                          8  double
         srate          1x1                          8  double
         timevec        1x661500               5292000  double

Total is 2315408 elements using 18522193 bytes

glassclip(1:10, 1)

ans	1
1	0
2	0
3	0
4	0
5	0
6	0
7	0
8	0
9	0
10	0

pow = abs(fft(glassclip(:,channel))/pnts); pow(1:10)

ans	1
1	0.00012627
2	1.48464e-06
3	1.33056e-06
4	1.18443e-06
5	8.39429e-07
6	1.03065e-06
7	1.79451e-06
8	1.46856e-06
9	1.05083e-06
10	1.43139e-06

whos

Variables visible from the current scope:

variables in scope: top scope

  Attr   Name           Size                     Bytes  Class
  ====   ====           ====                     =====  ===== 
         ans           10x1                         80  double
         channel        1x1                          8  double
         doc_file       1x84                        84  char
         glassclip 661500x2                   10584000  double
         hz             1x330751               2646008  double
         pkg_dir        1x69                        69  char
         pnts           1x1                          8  double
         pow       661500x1                    5292000  double
         srate          1x1                          8  double
         timevec        1x661500               5292000  double

Total is 2976917 elements using 23814265 bytes

figure(2), clf
subplot(311)
plot(timevec, glassclip)
xlabel('Time (s) ')

subplot(312), cla
plot(hz, pow(1:length(hz)))
xlabel('Frequency (Hz)' ), ylabel('Amplitude')

subplot(313), cla
plot(hz, pow(1:length(hz)))
set(gca, 'xlim', [100 2000], 'ylim', [0 max(pow)])
xlabel('Frequency Range Limited (Hz) '), ylabel('Amplitude')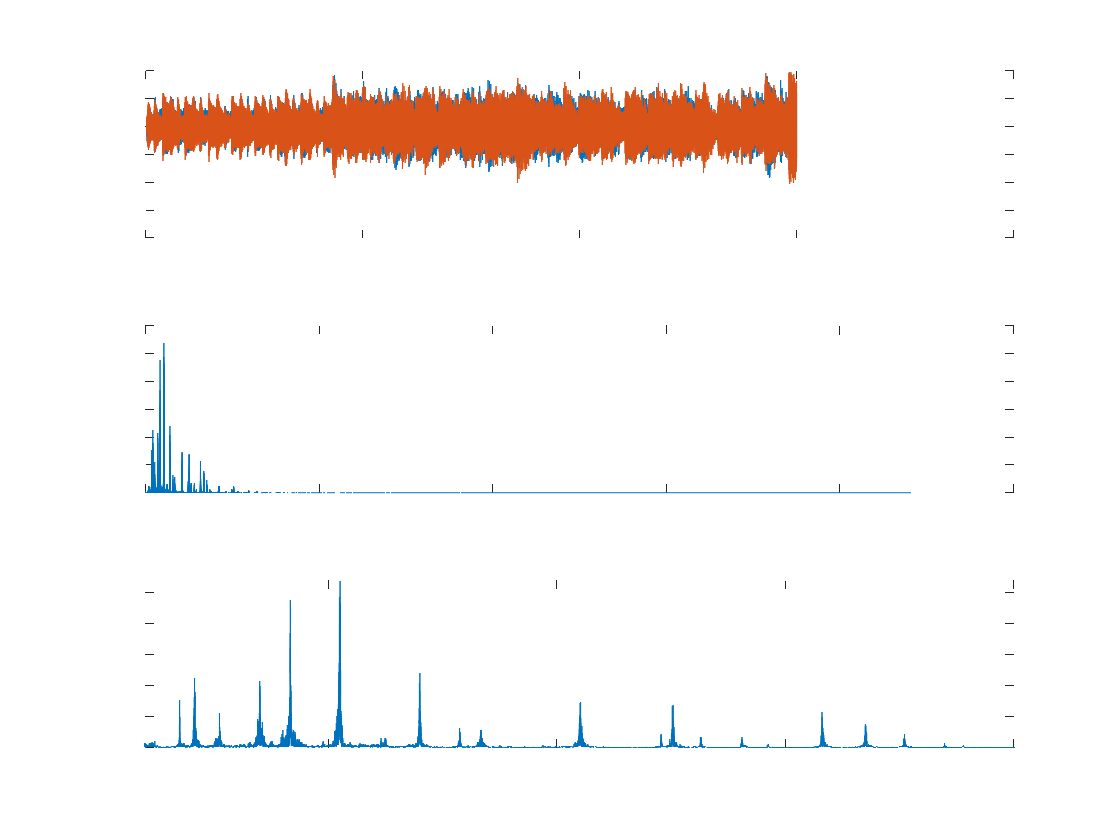

warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)

Design a FIR Filter

frange = [300 460]

frange	1	2
1	300	460

fkern = fir1(2001,frange/(srate/2),'bandpass');

fkern

fkern	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127	128	129	130	131	132	133	134	135	136	137	138	139	140	141	142	143	144	145	146	147	148	149	150	151	152	153	154	155	156	157	158	159	160	161	162	163	164	165	166	167	168	169	170	171	172	173	174	175	176	177	178	179	180	181	182	183	184	185	186	187	188	189	190	191	192	193	194	195	196	197	198	199	200	201	202	203	204	205	206	207	208	209	210	211	212	213	214	215	216	217	218	219	220	221	222	223	224	225	226	227	228	229	230	231	232	233	234	235	236	237	238	239	240	241	242	243	244	245	246	247	248	249	250	251	252	253	254	255	256	257	258	259	260	261	262	263	264	265	266	267	268	269	270	271	272	273	274	275	276	277	278	279	280	281	282	283	284	285	286	287	288	289	290	291	292	293	294	295	296	297	298	299	300	301	302	303	304	305	306	307	308	309	310	311	312	313	314	315	316	317	318	319	320	321	322	323	324	325	326	327	328	329	330	331	332	333	334	335	336	337	338	339	340	341	342	343	344	345	346	347	348	349	350	351	352	353	354	355	356	357	358	359	360	361	362	363	364	365	366	367	368	369	370	371	372	373	374	375	376	377	378	379	380	381	382	383	384	385	386	387	388	389	390	391	392	393	394	395	396	397	398	399	400	401	402	403	404	405	406	407	408	409	410	411	412	413	414	415	416	417	418	419	420	421	422	423	424	425	426	427	428	429	430	431	432	433	434	435	436	437	438	439	440	441	442	443	444	445	446	447	448	449	450	451	452	453	454	455	456	457	458	459	460	461	462	463	464	465	466	467	468	469	470	471	472	473	474	475	476	477	478	479	480	481	482	483	484	485	486	487	488	489	490	491	492	493	494	495	496	497	498	499	500	501	502	503	504	505	506	507	508	509	510	511	512	513	514	515	516	517	518	519	520	521	522	523	524	525	526	527	528	529	530	531	532	533	534	535	536	537	538	539	540	541	542	543	544	545	546	547	548	549	550	551	552	553	554	555	556	557	558	559	560	561	562	563	564	565	566	567	568	569	570	571	572	573	574	575	576	577	578	579	580	581	582	583	584	585	586	587	588	589	590	591	592	593	594	595	596	597	598	599	600	601	602	603	604	605	606	607	608	609	610	611	612	613	614	615	616	617	618	619	620	621	622	623	624	625	626	627	628	629	630	631	632	633	634	635	636	637	638	639	640	641	642	643	644	645	646	647	648	649	650	651	652	653	654	655	656	657	658	659	660	661	662	663	664	665	666	667	668	669	670	671	672	673	674	675	676	677	678	679	680	681	682	683	684	685	686	687	688	689	690	691	692	693	694	695	696	697	698	699	700	701	702	703	704	705	706	707	708	709	710	711	712	713	714	715	716	717	718	719	720	721	722	723	724	725	726	727	728	729	730	731	732	733	734	735	736	737	738	739	740	741	742	743	744	745	746	747	748	749	750	751	752	753	754	755	756	757	758	759	760	761	762	763	764	765	766	767	768	769	770	771	772	773	774	775	776	777	778	779	780	781	782	783	784	785	786	787	788	789	790	791	792	793	794	795	796	797	798	799	800	801	802	803	804	805	806	807	808	809	810	811	812	813	814	815	816	817	818	819	820	821	822	823	824	825	826	827	828	829	830	831	832	833	834	835	836	837	838	839	840	841	842	843	844	845	846	847	848	849	850	851	852	853	854	855	856	857	858	859	860	861	862	863	864	865	866	867	868	869	870	871	872	873	874	875	876	877	878	879	880	881	882	883	884	885	886	887	888	889	890	891	892	893	894	895	896	897	898	899	900	901	902	903	904	905	906	907	908	909	910	911	912	913	914	915	916	917	918	919	920	921	922	923	924	925	926	927	928	929	930	931	932	933	934	935	936	937	938	939	940	941	942	943	944	945	946	947	948	949	950	951	952	953	954	955	956	957	958	959	960	961	962	963	964	965	966	967	968	969	970	971	972	973	974	975	976	977	978	979	980	981	982	983	984	985	986	987	988	989	990	991	992	993	994	995	996	997	998	999	1000	1001	1002	1003	1004	1005	1006	1007	1008	1009	1010	1011	1012	1013	1014	1015	1016	1017	1018	1019	1020	1021	1022	1023	1024	1025	1026	1027	1028	1029	1030	1031	1032	1033	1034	1035	1036	1037	1038	1039	1040	1041	1042	1043	1044	1045	1046	1047	1048	1049	1050	1051	1052	1053	1054	1055	1056	1057	1058	1059	1060	1061	1062	1063	1064	1065	1066	1067	1068	1069	1070	1071	1072	1073	1074	1075	1076	1077	1078	1079	1080	1081	1082	1083	1084	1085	1086	1087	1088	1089	1090	1091	1092	1093	1094	1095	1096	1097	1098	1099	1100	1101	1102	1103	1104	1105	1106	1107	1108	1109	1110	1111	1112	1113	1114	1115	1116	1117	1118	1119	1120	1121	1122	1123	1124	1125	1126	1127	1128	1129	1130	1131	1132	1133	1134	1135	1136	1137	1138	1139	1140	1141	1142	1143	1144	1145	1146	1147	1148	1149	1150	1151	1152	1153	1154	1155	1156	1157	1158	1159	1160	1161	1162	1163	1164	1165	1166	1167	1168	1169	1170	1171	1172	1173	1174	1175	1176	1177	1178	1179	1180	1181	1182	1183	1184	1185	1186	1187	1188	1189	1190	1191	1192	1193	1194	1195	1196	1197	1198	1199	1200	1201	1202	1203	1204	1205	1206	1207	1208	1209	1210	1211	1212	1213	1214	1215	1216	1217	1218	1219	1220	1221	1222	1223	1224	1225	1226	1227	1228	1229	1230	1231	1232	1233	1234	1235	1236	1237	1238	1239	1240	1241	1242	1243	1244	1245	1246	1247	1248	1249	1250	1251	1252	1253	1254	1255	1256	1257	1258	1259	1260	1261	1262	1263	1264	1265	1266	1267	1268	1269	1270	1271	1272	1273	1274	1275	1276	1277	1278	1279	1280	1281	1282	1283	1284	1285	1286	1287	1288	1289	1290	1291	1292	1293	1294	1295	1296	1297	1298	1299	1300	1301	1302	1303	1304	1305	1306	1307	1308	1309	1310	1311	1312	1313	1314	1315	1316	1317	1318	1319	1320	1321	1322	1323	1324	1325	1326	1327	1328	1329	1330	1331	1332	1333	1334	1335	1336	1337	1338	1339	1340	1341	1342	1343	1344	1345	1346	1347	1348	1349	1350	1351	1352	1353	1354	1355	1356	1357	1358	1359	1360	1361	1362	1363	1364	1365	1366	1367	1368	1369	1370	1371	1372	1373	1374	1375	1376	1377	1378	1379	1380	1381	1382	1383	1384	1385	1386	1387	1388	1389	1390	1391	1392	1393	1394	1395	1396	1397	1398	1399	1400	1401	1402	1403	1404	1405	1406	1407	1408	1409	1410	1411	1412	1413	1414	1415	1416	1417	1418	1419	1420	1421	1422	1423	1424	1425	1426	1427	1428	1429	1430	1431	1432	1433	1434	1435	1436	1437	1438	1439	1440	1441	1442	1443	1444	1445	1446	1447	1448	1449	1450	1451	1452	1453	1454	1455	1456	1457	1458	1459	1460	1461	1462	1463	1464	1465	1466	1467	1468	1469	1470	1471	1472	1473	1474	1475	1476	1477	1478	1479	1480	1481	1482	1483	1484	1485	1486	1487	1488	1489	1490	1491	1492	1493	1494	1495	1496	1497	1498	1499	1500	1501	1502	1503	1504	1505	1506	1507	1508	1509	1510	1511	1512	1513	1514	1515	1516	1517	1518	1519	1520	1521	1522	1523	1524	1525	1526	1527	1528	1529	1530	1531	1532	1533	1534	1535	1536	1537	1538	1539	1540	1541	1542	1543	1544	1545	1546	1547	1548	1549	1550	1551	1552	1553	1554	1555	1556	1557	1558	1559	1560	1561	1562	1563	1564	1565	1566	1567	1568	1569	1570	1571	1572	1573	1574	1575	1576	1577	1578	1579	1580	1581	1582	1583	1584	1585	1586	1587	1588	1589	1590	1591	1592	1593	1594	1595	1596	1597	1598	1599	1600	1601	1602	1603	1604	1605	1606	1607	1608	1609	1610	1611	1612	1613	1614	1615	1616	1617	1618	1619	1620	1621	1622	1623	1624	1625	1626	1627	1628	1629	1630	1631	1632	1633	1634	1635	1636	1637	1638	1639	1640	1641	1642	1643	1644	1645	1646	1647	1648	1649	1650	1651	1652	1653	1654	1655	1656	1657	1658	1659	1660	1661	1662	1663	1664	1665	1666	1667	1668	1669	1670	1671	1672	1673	1674	1675	1676	1677	1678	1679	1680	1681	1682	1683	1684	1685	1686	1687	1688	1689	1690	1691	1692	1693	1694	1695	1696	1697	1698	1699	1700	1701	1702	1703	1704	1705	1706	1707	1708	1709	1710	1711	1712	1713	1714	1715	1716	1717	1718	1719	1720	1721	1722	1723	1724	1725	1726	1727	1728	1729	1730	1731	1732	1733	1734	1735	1736	1737	1738	1739	1740	1741	1742	1743	1744	1745	1746	1747	1748	1749	1750	1751	1752	1753	1754	1755	1756	1757	1758	1759	1760	1761	1762	1763	1764	1765	1766	1767	1768	1769	1770	1771	1772	1773	1774	1775	1776	1777	1778	1779	1780	1781	1782	1783	1784	1785	1786	1787	1788	1789	1790	1791	1792	1793	1794	1795	1796	1797	1798	1799	1800	1801	1802	1803	1804	1805	1806	1807	1808	1809	1810	1811	1812	1813	1814	1815	1816	1817	1818	1819	1820	1821	1822	1823	1824	1825	1826	1827	1828	1829	1830	1831	1832	1833	1834	1835	1836	1837	1838	1839	1840	1841	1842	1843	1844	1845	1846	1847	1848	1849	1850	1851	1852	1853	1854	1855	1856	1857	1858	1859	1860	1861	1862	1863	1864	1865	1866	1867	1868	1869	1870	1871	1872	1873	1874	1875	1876	1877	1878	1879	1880	1881	1882	1883	1884	1885	1886	1887	1888	1889	1890	1891	1892	1893	1894	1895	1896	1897	1898	1899	1900	1901	1902	1903	1904	1905	1906	1907	1908	1909	1910	1911	1912	1913	1914	1915	1916	1917	1918	1919	1920	1921	1922	1923	1924	1925	1926	1927	1928	1929	1930	1931	1932	1933	1934	1935	1936	1937	1938	1939	1940	1941	1942	1943	1944	1945	1946	1947	1948	1949	1950	1951	1952	1953	1954	1955	1956	1957	1958	1959	1960	1961	1962	1963	1964	1965	1966	1967	1968	1969	1970	1971	1972	1973	1974	1975	1976	1977	1978	1979	1980	1981	1982	1983	1984	1985	1986	1987	1988	1989	1990	1991	1992	1993	1994	1995	1996	1997	1998	1999	2000	2001	2002
1	4.29162e-05	4.31808e-05	4.33219e-05	4.33379e-05	4.32271e-05	4.29886e-05	4.26215e-05	4.21256e-05	4.1501e-05	4.07483e-05	3.98685e-05	3.8863e-05	3.77335e-05	3.64824e-05	3.51122e-05	3.3626e-05	3.20273e-05	3.03199e-05	2.85081e-05	2.65964e-05	2.45899e-05	2.24938e-05	2.03139e-05	1.8056e-05	1.57265e-05	1.33318e-05	1.08788e-05	8.37455e-06	5.82629e-06	3.24149e-06	6.27785e-07	-2.00704e-06	-4.65507e-06	-7.3083e-06	-9.95864e-06	-1.2598e-05	-1.52181e-05	-1.78109e-05	-2.03683e-05	-2.28823e-05	-2.53447e-05	-2.77479e-05	-3.00841e-05	-3.23457e-05	-3.45254e-05	-3.66161e-05	-3.86109e-05	-4.05033e-05	-4.22868e-05	-4.39555e-05	-4.55038e-05	-4.69263e-05	-4.82182e-05	-4.93749e-05	-5.03924e-05	-5.1267e-05	-5.19955e-05	-5.25751e-05	-5.30037e-05	-5.32793e-05	-5.34008e-05	-5.33673e-05	-5.31787e-05	-5.2835e-05	-5.23372e-05	-5.16863e-05	-5.08843e-05	-4.99334e-05	-4.88364e-05	-4.75966e-05	-4.62177e-05	-4.4704e-05	-4.30602e-05	-4.12915e-05	-3.94034e-05	-3.74019e-05	-3.52935e-05	-3.30849e-05	-3.07832e-05	-2.83959e-05	-2.59307e-05	-2.33956e-05	-2.07989e-05	-1.81491e-05	-1.54548e-05	-1.27249e-05	-9.96831e-06	-7.19403e-06	-4.41119e-06	-1.62889e-06	1.14376e-06	3.8977e-06	6.62394e-06	9.31361e-06	1.1958e-05	1.45485e-05	1.70769e-05	1.95349e-05	2.19149e-05	2.42094e-05	2.6411e-05	2.85131e-05	3.05092e-05	3.23933e-05	3.41599e-05	3.58039e-05	3.73206e-05	3.8706e-05	3.99566e-05	4.10691e-05	4.20413e-05	4.28711e-05	4.35572e-05	4.40988e-05	4.44957e-05	4.47483e-05	4.48575e-05	4.48249e-05	4.46525e-05	4.43431e-05	4.38999e-05	4.33265e-05	4.26274e-05	4.18073e-05	4.08714e-05	3.98255e-05	3.86758e-05	3.74288e-05	3.60916e-05	3.46713e-05	3.31757e-05	3.16127e-05	2.99904e-05	2.83173e-05	2.66018e-05	2.48527e-05	2.30788e-05	2.12888e-05	1.94917e-05	1.76963e-05	1.59113e-05	1.41454e-05	1.2407e-05	1.07045e-05	9.0458e-06	7.4388e-06	5.89092e-06	4.40924e-06	3.00049e-06	1.67094e-06	4.26393e-07	-7.27811e-07	-1.78688e-06	-2.74656e-06	-3.60318e-06	-4.35368e-06	-4.99559e-06	-5.5271e-06	-5.94705e-06	-6.25495e-06	-6.45096e-06	-6.53593e-06	-6.51141e-06	-6.3796e-06	-6.14338e-06	-5.80632e-06	-5.37263e-06	-4.84717e-06	-4.2354e-06	-3.54342e-06	-2.7779e-06	-1.94604e-06	-1.05559e-06	-1.14782e-07	8.67708e-07	1.88278e-06	2.92098e-06	3.9725e-06	5.02726e-06	6.07497e-06	7.10512e-06	8.1071e-06	9.07021e-06	9.98373e-06	1.0837e-05	1.16194e-05	1.23205e-05	1.29301e-05	1.34382e-05	1.38351e-05	1.41116e-05	1.4259e-05	1.42687e-05	1.41332e-05	1.38451e-05	1.33979e-05	1.27859e-05	1.20038e-05	1.10474e-05	9.91324e-06	8.59867e-06	7.10198e-06	5.42238e-06	3.56005e-06	1.51613e-06	-7.07227e-07	-3.10686e-06	-5.67859e-06	-8.4172e-06	-1.13165e-05	-1.43691e-05	-1.75668e-05	-2.09004e-05	-2.43596e-05	-2.79331e-05	-3.16088e-05	-3.53736e-05	-3.92137e-05	-4.31143e-05	-4.706e-05	-5.10345e-05	-5.50209e-05	-5.90018e-05	-6.29593e-05	-6.68747e-05	-7.07293e-05	-7.45039e-05	-7.81789e-05	-8.1735e-05	-8.51522e-05	-8.84111e-05	-9.1492e-05	-9.43754e-05	-9.70424e-05	-9.9474e-05	-0.000101652	-0.000103559	-0.000105177	-0.00010649	-0.000107482	-0.000108139	-0.000108447	-0.000108392	-0.000107965	-0.000107153	-0.000105948	-0.000104342	-0.000102329	-9.99042e-05	-9.70636e-05	-9.38055e-05	-9.01298e-05	-8.60378e-05	-8.15326e-05	-7.66191e-05	-7.13036e-05	-6.55943e-05	-5.95011e-05	-5.30358e-05	-4.62115e-05	-3.90433e-05	-3.15478e-05	-2.37435e-05	-1.56501e-05	-7.28903e-06	1.31674e-06	1.01429e-05	1.91638e-05	2.83525e-05	3.76808e-05	4.71195e-05	5.66383e-05	6.6206e-05	7.57907e-05	8.53597e-05	9.48796e-05	0.000104317	0.000113637	0.000122807	0.000131791	0.000140555	0.000149066	0.000157288	0.00016519	0.000172737	0.000179899	0.000186644	0.000192941	0.000198761	0.000204077	0.000208862	0.00021309	0.00021674	0.000219788	0.000222215	0.000224003	0.000225136	0.0002256	0.000225383	0.000224477	0.000222874	0.000220569	0.00021756	0.000213848	0.000209435	0.000204326	0.000198529	0.000192055	0.000184916	0.000177128	0.000168709	0.000159678	0.000150059	0.000139877	0.000129158	0.000117932	0.000106232	9.4089e-05	8.15402e-05	6.86224e-05	5.53743e-05	4.18364e-05	2.80505e-05	1.40596e-05	-9.22056e-08	-1.43599e-05	-2.86976e-05	-4.30588e-05	-5.73968e-05	-7.16644e-05	-8.58143e-05	-9.97994e-05	-0.000113573	-0.000127088	-0.000140299	-0.000153162	-0.000165631	-0.000177664	-0.00018922	-0.000200259	-0.000210741	-0.000220631	-0.000229893	-0.000238496	-0.000246408	-0.000253602	-0.000260052	-0.000265735	-0.000270631	-0.000274723	-0.000277996	-0.000280438	-0.00028204	-0.000282798	-0.000282708	-0.00028177	-0.000279989	-0.000277371	-0.000273926	-0.000269666	-0.000264608	-0.000258769	-0.000252173	-0.000244843	-0.000236806	-0.000228092	-0.000218733	-0.000208765	-0.000198223	-0.000187147	-0.000175579	-0.000163559	-0.000151134	-0.000138348	-0.000125249	-0.000111885	-9.83045e-05	-8.45573e-05	-7.06936e-05	-5.67636e-05	-4.28178e-05	-2.89063e-05	-1.5079e-05	-1.38529e-06	1.21265e-05	2.54088e-05	3.84153e-05	5.11011e-05	6.34228e-05	7.53388e-05	8.68095e-05	9.77973e-05	0.000108267	0.000118186	0.000127523	0.000136251	0.000144345	0.000151784	0.000158548	0.000164622	0.000169993	0.000174651	0.000178591	0.000181809	0.000184306	0.000186086	0.000187154	0.000187523	0.000187204	0.000186215	0.000184575	0.000182306	0.000179434	0.000175987	0.000171994	0.00016749	0.00016251	0.00015709	0.000151271	0.000145093	0.000138599	0.000131833	0.000124841	0.000117667	0.000110359	0.000102964	9.55296e-05	8.81024e-05	8.07296e-05	7.34578e-05	6.63328e-05	5.93992e-05	5.27007e-05	4.62793e-05	4.01755e-05	3.44277e-05	2.90726e-05	2.4144e-05	1.96738e-05	1.56908e-05	1.22212e-05	9.28812e-06	6.91142e-06	5.10779e-06	3.89051e-06	3.26932e-06	3.25041e-06	3.83628e-06	5.02572e-06	6.8138e-06	9.19179e-06	1.21472e-05	1.56639e-05	1.97219e-05	2.42977e-05	2.9364e-05	3.48904e-05	4.08428e-05	4.71839e-05	5.38736e-05	6.08683e-05	6.81223e-05	7.55869e-05	8.32111e-05	9.09419e-05	9.87244e-05	0.000106502	0.000114217	0.000121809	0.00012922	0.000136389	0.000143255	0.000149756	0.000155834	0.000161429	0.000166481	0.000170934	0.000174731	0.00017782	0.000180147	0.000181665	0.000182326	0.000182087	0.000180909	0.000178755	0.000175593	0.000171394	0.000166133	0.000159793	0.000152356	0.000143814	0.000134162	0.000123399	0.00011153	9.85676e-05	8.45264e-05	6.94284e-05	5.33005e-05	3.61751e-05	1.809e-05	-9.11402e-07	-2.07807e-05	-4.14643e-05	-6.29034e-05	-8.50344e-05	-0.000107789	-0.000131094	-0.000154873	-0.000179044	-0.000203523	-0.00022822	-0.000253045	-0.000277902	-0.000302695	-0.000327325	-0.00035169	-0.000375688	-0.000399217	-0.000422171	-0.000444448	-0.000465943	-0.000486553	-0.000506176	-0.000524712	-0.000542063	-0.000558134	-0.00057283	-0.000586062	-0.000597745	-0.000607798	-0.000616142	-0.000622706	-0.000627423	-0.000630233	-0.000631079	-0.000629914	-0.000626696	-0.000621389	-0.000613966	-0.000604406	-0.000592696	-0.000578832	-0.000562817	-0.000544661	-0.000524384	-0.000502013	-0.000477583	-0.00045114	-0.000422733	-0.000392425	-0.000360282	-0.00032638	-0.000290803	-0.000253642	-0.000214996	-0.000174968	-0.000133671	-9.12234e-05	-4.77482e-05	-3.37511e-06	4.17612e-05	8.75215e-05	0.000133762	0.000180337	0.000227094	0.000273881	0.000320543	0.000366923	0.000412863	0.000458205	0.000502791	0.000546463	0.000589065	0.000630443	0.000670445	0.000708924	0.000745734	0.000780735	0.00081379	0.000844771	0.000873553	0.000900017	0.000924053	0.000945557	0.000964434	0.000980597	0.000993968	0.00100448	0.00101206	0.00101667	0.00101827	0.00101683	0.00101233	0.00100475	0.000994101	0.000980396	0.000963656	0.000943915	0.000921218	0.000895619	0.000867186	0.000835993	0.000802127	0.000765685	0.000726771	0.000685501	0.000641998	0.000596394	0.000548831	0.000499454	0.000448419	0.000395888	0.000342027	0.000287008	0.000231008	0.000174209	0.000116795	5.89526e-05	8.71419e-07	-5.72583e-05	-0.000115246	-0.0001729	-0.00023003	-0.000286449	-0.00034197	-0.00039641	-0.000449589	-0.000501332	-0.00055147	-0.000599839	-0.000646279	-0.000690641	-0.00073278	-0.000772563	-0.000809862	-0.000844559	-0.000876548	-0.000905731	-0.00093202	-0.000955339	-0.000975623	-0.000992818	-0.00100688	-0.00101778	-0.0010255	-0.00103004	-0.00103139	-0.00102958	-0.00102463	-0.00101658	-0.0010055	-0.000991434	-0.000974467	-0.000954683	-0.000932178	-0.000907058	-0.000879439	-0.000849448	-0.000817216	-0.000782886	-0.000746608	-0.000708537	-0.000668836	-0.000627672	-0.000585218	-0.000541651	-0.000497149	-0.000451896	-0.000406076	-0.000359873	-0.000313473	-0.00026706	-0.000220818	-0.000174927	-0.000129565	-8.49058e-05	-4.11196e-05	1.62974e-06	4.3184e-05	8.33917e-05	0.000122109	0.000159199	0.000194535	0.000227998	0.00025948	0.000288882	0.000316117	0.000341107	0.000363788	0.000384106	0.000402018	0.000417496	0.000430522	0.000441091	0.00044921	0.000454899	0.00045819	0.000459127	0.000457766	0.000454174	0.000448431	0.000440627	0.000430863	0.000419249	0.000405905	0.00039096	0.000374554	0.000356831	0.000337944	0.000318051	0.000297318	0.000275914	0.000254013	0.00023179	0.000209424	0.000187095	0.000164984	0.000143271	0.000122134	0.000101749	8.22889e-05	6.39229e-05	4.68146e-05	3.11214e-05	1.69944e-05	4.57652e-06	-5.99748e-06	-1.46023e-05	-2.11227e-05	-2.54541e-05	-2.75036e-05	-2.71902e-05	-2.44456e-05	-1.92147e-05	-1.14561e-05	-1.14251e-06	1.1739e-05	2.71865e-05	4.51832e-05	6.56972e-05	8.86813e-05	0.000114073	0.000141795	0.000171754	0.000203843	0.000237939	0.000273907	0.000311594	0.000350838	0.000391462	0.000433276	0.00047608	0.000519661	0.000563799	0.000608262	0.000652811	0.000697198	0.000741171	0.000784472	0.000826837	0.000868	0.000907695	0.000945652	0.000981603	0.00101528	0.00104643	0.00107478	0.00110008	0.00112208	0.00114056	0.00115526	0.00116599	0.00117252	0.00117467	0.00117225	0.0011651	0.00115307	0.00113602	0.00111384	0.00108644	0.00105374	0.00101567	0.000972217	0.000923357	0.000869102	0.000809484	0.000744559	0.000674404	0.000599123	0.000518842	0.000433709	0.000343898	0.000249604	0.000151048	4.84705e-05	-5.7864e-05	-0.00016767	-0.000280642	-0.000396454	-0.00051476	-0.000635196	-0.000757383	-0.000880923	-0.00100541	-0.00113041	-0.00125549	-0.0013802	-0.0015041	-0.00162671	-0.00174756	-0.00186618	-0.00198209	-0.00209482	-0.0022039	-0.00230884	-0.00240918	-0.00250446	-0.00259422	-0.00267802	-0.00275544	-0.00282605	-0.00288945	-0.00294527	-0.00299313	-0.00303269	-0.00306363	-0.00308566	-0.0030985	-0.00310192	-0.00309568	-0.00307962	-0.00305357	-0.00301742	-0.00297106	-0.00291445	-0.00284757	-0.00277042	-0.00268306	-0.00258557	-0.00247808	-0.00236074	-0.00223375	-0.00209734	-0.00195178	-0.00179736	-0.00163444	-0.00146338	-0.00128459	-0.00109851	-0.00090561	-0.000706396	-0.0005014	-0.00029118	-7.63243e-05	0.000142557	0.00036483	0.00058984	0.000816911	0.00104535	0.00127446	0.00150351	0.00173177	0.00195852	0.002183	0.00240446	0.00262217	0.00283538	0.00304334	0.00324532	0.00344061	0.00362848	0.00380824	0.00397921	0.00414073	0.00429217	0.00443291	0.00456236	0.00467997	0.00478522	0.00487761	0.00495669	0.00502204	0.00507328	0.00511007	0.00513213	0.00513919	0.00513107	0.00510759	0.00506864	0.00501418	0.00494418	0.00485868	0.00475777	0.00464158	0.00451031	0.0043642	0.00420353	0.00402863	0.00383991	0.00363779	0.00342276	0.00319534	0.00295611	0.00270568	0.00244472	0.00217391	0.00189399	0.00160574	0.00130996	0.00100748	0.000699164	0.000385908	6.86214e-05	-0.000251761	-0.000574289	-0.000897995	-0.0012219	-0.00154502	-0.00186637	-0.00218494	-0.00249975	-0.00280981	-0.00311413	-0.00341175	-0.00370171	-0.00398307	-0.00425491	-0.00451633	-0.00476647	-0.00500448	-0.00522956	-0.00544094	-0.00563787	-0.00581968	-0.0059857	-0.00613533	-0.00626801	-0.00638324	-0.00648055	-0.00655955	-0.00661988	-0.00666126	-0.00668344	-0.00668625	-0.00666958	-0.00663337	-0.00657761	-0.00650239	-0.00640782	-0.00629408	-0.00616144	-0.00601019	-0.0058407	-0.0056534	-0.00544877	-0.00522734	-0.00498972	-0.00473654	-0.00446851	-0.00418637	-0.00389091	-0.00358296	-0.00326342	-0.00293319	-0.00259323	-0.00224452	-0.00188809	-0.00152498	-0.00115626	-0.00078302	-0.000406364	-2.74142e-05	0.000352698	0.000732834	0.00111185	0.00148862	0.00186199	0.00223085	0.00259406	0.00295054	0.0032992	0.00363898	0.00396884	0.00428778	0.00459483	0.00488904	0.00516951	0.00543538	0.00568585	0.00592013	0.00613752	0.00633733	0.00651896	0.00668185	0.00682549	0.00694944	0.00705333	0.00713683	0.00719967	0.00724168	0.00726272	0.00726272	0.00724168	0.00719967	0.00713683	0.00705333	0.00694944	0.00682549	0.00668185	0.00651896	0.00633733	0.00613752	0.00592013	0.00568585	0.00543538	0.00516951	0.00488904	0.00459483	0.00428778	0.00396884	0.00363898	0.0032992	0.00295054	0.00259406	0.00223085	0.00186199	0.00148862	0.00111185	0.000732834	0.000352698	-2.74142e-05	-0.000406364	-0.00078302	-0.00115626	-0.00152498	-0.00188809	-0.00224452	-0.00259323	-0.00293319	-0.00326342	-0.00358296	-0.00389091	-0.00418637	-0.00446851	-0.00473654	-0.00498972	-0.00522734	-0.00544877	-0.0056534	-0.0058407	-0.00601019	-0.00616144	-0.00629408	-0.00640782	-0.00650239	-0.00657761	-0.00663337	-0.00666958	-0.00668625	-0.00668344	-0.00666126	-0.00661988	-0.00655955	-0.00648055	-0.00638324	-0.00626801	-0.00613533	-0.0059857	-0.00581968	-0.00563787	-0.00544094	-0.00522956	-0.00500448	-0.00476647	-0.00451633	-0.00425491	-0.00398307	-0.00370171	-0.00341175	-0.00311413	-0.00280981	-0.00249975	-0.00218494	-0.00186637	-0.00154502	-0.0012219	-0.000897995	-0.000574289	-0.000251761	6.86214e-05	0.000385908	0.000699164	0.00100748	0.00130996	0.00160574	0.00189399	0.00217391	0.00244472	0.00270568	0.00295611	0.00319534	0.00342276	0.00363779	0.00383991	0.00402863	0.00420353	0.0043642	0.00451031	0.00464158	0.00475777	0.00485868	0.00494418	0.00501418	0.00506864	0.00510759	0.00513107	0.00513919	0.00513213	0.00511007	0.00507328	0.00502204	0.00495669	0.00487761	0.00478522	0.00467997	0.00456236	0.00443291	0.00429217	0.00414073	0.00397921	0.00380824	0.00362848	0.00344061	0.00324532	0.00304334	0.00283538	0.00262217	0.00240446	0.002183	0.00195852	0.00173177	0.00150351	0.00127446	0.00104535	0.000816911	0.00058984	0.00036483	0.000142557	-7.63243e-05	-0.00029118	-0.0005014	-0.000706396	-0.00090561	-0.00109851	-0.00128459	-0.00146338	-0.00163444	-0.00179736	-0.00195178	-0.00209734	-0.00223375	-0.00236074	-0.00247808	-0.00258557	-0.00268306	-0.00277042	-0.00284757	-0.00291445	-0.00297106	-0.00301742	-0.00305357	-0.00307962	-0.00309568	-0.00310192	-0.0030985	-0.00308566	-0.00306363	-0.00303269	-0.00299313	-0.00294527	-0.00288945	-0.00282605	-0.00275544	-0.00267802	-0.00259422	-0.00250446	-0.00240918	-0.00230884	-0.0022039	-0.00209482	-0.00198209	-0.00186618	-0.00174756	-0.00162671	-0.0015041	-0.0013802	-0.00125549	-0.00113041	-0.00100541	-0.000880923	-0.000757383	-0.000635196	-0.00051476	-0.000396454	-0.000280642	-0.00016767	-5.7864e-05	4.84705e-05	0.000151048	0.000249604	0.000343898	0.000433709	0.000518842	0.000599123	0.000674404	0.000744559	0.000809484	0.000869102	0.000923357	0.000972217	0.00101567	0.00105374	0.00108644	0.00111384	0.00113602	0.00115307	0.0011651	0.00117225	0.00117467	0.00117252	0.00116599	0.00115526	0.00114056	0.00112208	0.00110008	0.00107478	0.00104643	0.00101528	0.000981603	0.000945652	0.000907695	0.000868	0.000826837	0.000784472	0.000741171	0.000697198	0.000652811	0.000608262	0.000563799	0.000519661	0.00047608	0.000433276	0.000391462	0.000350838	0.000311594	0.000273907	0.000237939	0.000203843	0.000171754	0.000141795	0.000114073	8.86813e-05	6.56972e-05	4.51832e-05	2.71865e-05	1.1739e-05	-1.14251e-06	-1.14561e-05	-1.92147e-05	-2.44456e-05	-2.71902e-05	-2.75036e-05	-2.54541e-05	-2.11227e-05	-1.46023e-05	-5.99748e-06	4.57652e-06	1.69944e-05	3.11214e-05	4.68146e-05	6.39229e-05	8.22889e-05	0.000101749	0.000122134	0.000143271	0.000164984	0.000187095	0.000209424	0.00023179	0.000254013	0.000275914	0.000297318	0.000318051	0.000337944	0.000356831	0.000374554	0.00039096	0.000405905	0.000419249	0.000430863	0.000440627	0.000448431	0.000454174	0.000457766	0.000459127	0.00045819	0.000454899	0.00044921	0.000441091	0.000430522	0.000417496	0.000402018	0.000384106	0.000363788	0.000341107	0.000316117	0.000288882	0.00025948	0.000227998	0.000194535	0.000159199	0.000122109	8.33917e-05	4.3184e-05	1.62974e-06	-4.11196e-05	-8.49058e-05	-0.000129565	-0.000174927	-0.000220818	-0.00026706	-0.000313473	-0.000359873	-0.000406076	-0.000451896	-0.000497149	-0.000541651	-0.000585218	-0.000627672	-0.000668836	-0.000708537	-0.000746608	-0.000782886	-0.000817216	-0.000849448	-0.000879439	-0.000907058	-0.000932178	-0.000954683	-0.000974467	-0.000991434	-0.0010055	-0.00101658	-0.00102463	-0.00102958	-0.00103139	-0.00103004	-0.0010255	-0.00101778	-0.00100688	-0.000992818	-0.000975623	-0.000955339	-0.00093202	-0.000905731	-0.000876548	-0.000844559	-0.000809862	-0.000772563	-0.00073278	-0.000690641	-0.000646279	-0.000599839	-0.00055147	-0.000501332	-0.000449589	-0.00039641	-0.00034197	-0.000286449	-0.00023003	-0.0001729	-0.000115246	-5.72583e-05	8.71419e-07	5.89526e-05	0.000116795	0.000174209	0.000231008	0.000287008	0.000342027	0.000395888	0.000448419	0.000499454	0.000548831	0.000596394	0.000641998	0.000685501	0.000726771	0.000765685	0.000802127	0.000835993	0.000867186	0.000895619	0.000921218	0.000943915	0.000963656	0.000980396	0.000994101	0.00100475	0.00101233	0.00101683	0.00101827	0.00101667	0.00101206	0.00100448	0.000993968	0.000980597	0.000964434	0.000945557	0.000924053	0.000900017	0.000873553	0.000844771	0.00081379	0.000780735	0.000745734	0.000708924	0.000670445	0.000630443	0.000589065	0.000546463	0.000502791	0.000458205	0.000412863	0.000366923	0.000320543	0.000273881	0.000227094	0.000180337	0.000133762	8.75215e-05	4.17612e-05	-3.37511e-06	-4.77482e-05	-9.12234e-05	-0.000133671	-0.000174968	-0.000214996	-0.000253642	-0.000290803	-0.00032638	-0.000360282	-0.000392425	-0.000422733	-0.00045114	-0.000477583	-0.000502013	-0.000524384	-0.000544661	-0.000562817	-0.000578832	-0.000592696	-0.000604406	-0.000613966	-0.000621389	-0.000626696	-0.000629914	-0.000631079	-0.000630233	-0.000627423	-0.000622706	-0.000616142	-0.000607798	-0.000597745	-0.000586062	-0.00057283	-0.000558134	-0.000542063	-0.000524712	-0.000506176	-0.000486553	-0.000465943	-0.000444448	-0.000422171	-0.000399217	-0.000375688	-0.00035169	-0.000327325	-0.000302695	-0.000277902	-0.000253045	-0.00022822	-0.000203523	-0.000179044	-0.000154873	-0.000131094	-0.000107789	-8.50344e-05	-6.29034e-05	-4.14643e-05	-2.07807e-05	-9.11402e-07	1.809e-05	3.61751e-05	5.33005e-05	6.94284e-05	8.45264e-05	9.85676e-05	0.00011153	0.000123399	0.000134162	0.000143814	0.000152356	0.000159793	0.000166133	0.000171394	0.000175593	0.000178755	0.000180909	0.000182087	0.000182326	0.000181665	0.000180147	0.00017782	0.000174731	0.000170934	0.000166481	0.000161429	0.000155834	0.000149756	0.000143255	0.000136389	0.00012922	0.000121809	0.000114217	0.000106502	9.87244e-05	9.09419e-05	8.32111e-05	7.55869e-05	6.81223e-05	6.08683e-05	5.38736e-05	4.71839e-05	4.08428e-05	3.48904e-05	2.9364e-05	2.42977e-05	1.97219e-05	1.56639e-05	1.21472e-05	9.19179e-06	6.8138e-06	5.02572e-06	3.83628e-06	3.25041e-06	3.26932e-06	3.89051e-06	5.10779e-06	6.91142e-06	9.28812e-06	1.22212e-05	1.56908e-05	1.96738e-05	2.4144e-05	2.90726e-05	3.44277e-05	4.01755e-05	4.62793e-05	5.27007e-05	5.93992e-05	6.63328e-05	7.34578e-05	8.07296e-05	8.81024e-05	9.55296e-05	0.000102964	0.000110359	0.000117667	0.000124841	0.000131833	0.000138599	0.000145093	0.000151271	0.00015709	0.00016251	0.00016749	0.000171994	0.000175987	0.000179434	0.000182306	0.000184575	0.000186215	0.000187204	0.000187523	0.000187154	0.000186086	0.000184306	0.000181809	0.000178591	0.000174651	0.000169993	0.000164622	0.000158548	0.000151784	0.000144345	0.000136251	0.000127523	0.000118186	0.000108267	9.77973e-05	8.68095e-05	7.53388e-05	6.34228e-05	5.11011e-05	3.84153e-05	2.54088e-05	1.21265e-05	-1.38529e-06	-1.5079e-05	-2.89063e-05	-4.28178e-05	-5.67636e-05	-7.06936e-05	-8.45573e-05	-9.83045e-05	-0.000111885	-0.000125249	-0.000138348	-0.000151134	-0.000163559	-0.000175579	-0.000187147	-0.000198223	-0.000208765	-0.000218733	-0.000228092	-0.000236806	-0.000244843	-0.000252173	-0.000258769	-0.000264608	-0.000269666	-0.000273926	-0.000277371	-0.000279989	-0.00028177	-0.000282708	-0.000282798	-0.00028204	-0.000280438	-0.000277996	-0.000274723	-0.000270631	-0.000265735	-0.000260052	-0.000253602	-0.000246408	-0.000238496	-0.000229893	-0.000220631	-0.000210741	-0.000200259	-0.00018922	-0.000177664	-0.000165631	-0.000153162	-0.000140299	-0.000127088	-0.000113573	-9.97994e-05	-8.58143e-05	-7.16644e-05	-5.73968e-05	-4.30588e-05	-2.86976e-05	-1.43599e-05	-9.22056e-08	1.40596e-05	2.80505e-05	4.18364e-05	5.53743e-05	6.86224e-05	8.15402e-05	9.4089e-05	0.000106232	0.000117932	0.000129158	0.000139877	0.000150059	0.000159678	0.000168709	0.000177128	0.000184916	0.000192055	0.000198529	0.000204326	0.000209435	0.000213848	0.00021756	0.000220569	0.000222874	0.000224477	0.000225383	0.0002256	0.000225136	0.000224003	0.000222215	0.000219788	0.00021674	0.00021309	0.000208862	0.000204077	0.000198761	0.000192941	0.000186644	0.000179899	0.000172737	0.00016519	0.000157288	0.000149066	0.000140555	0.000131791	0.000122807	0.000113637	0.000104317	9.48796e-05	8.53597e-05	7.57907e-05	6.6206e-05	5.66383e-05	4.71195e-05	3.76808e-05	2.83525e-05	1.91638e-05	1.01429e-05	1.31674e-06	-7.28903e-06	-1.56501e-05	-2.37435e-05	-3.15478e-05	-3.90433e-05	-4.62115e-05	-5.30358e-05	-5.95011e-05	-6.55943e-05	-7.13036e-05	-7.66191e-05	-8.15326e-05	-8.60378e-05	-9.01298e-05	-9.38055e-05	-9.70636e-05	-9.99042e-05	-0.000102329	-0.000104342	-0.000105948	-0.000107153	-0.000107965	-0.000108392	-0.000108447	-0.000108139	-0.000107482	-0.00010649	-0.000105177	-0.000103559	-0.000101652	-9.9474e-05	-9.70424e-05	-9.43754e-05	-9.1492e-05	-8.84111e-05	-8.51522e-05	-8.1735e-05	-7.81789e-05	-7.45039e-05	-7.07293e-05	-6.68747e-05	-6.29593e-05	-5.90018e-05	-5.50209e-05	-5.10345e-05	-4.706e-05	-4.31143e-05	-3.92137e-05	-3.53736e-05	-3.16088e-05	-2.79331e-05	-2.43596e-05	-2.09004e-05	-1.75668e-05	-1.43691e-05	-1.13165e-05	-8.4172e-06	-5.67859e-06	-3.10686e-06	-7.07227e-07	1.51613e-06	3.56005e-06	5.42238e-06	7.10198e-06	8.59867e-06	9.91324e-06	1.10474e-05	1.20038e-05	1.27859e-05	1.33979e-05	1.38451e-05	1.41332e-05	1.42687e-05	1.4259e-05	1.41116e-05	1.38351e-05	1.34382e-05	1.29301e-05	1.23205e-05	1.16194e-05	1.0837e-05	9.98373e-06	9.07021e-06	8.1071e-06	7.10512e-06	6.07497e-06	5.02726e-06	3.9725e-06	2.92098e-06	1.88278e-06	8.67708e-07	-1.14782e-07	-1.05559e-06	-1.94604e-06	-2.7779e-06	-3.54342e-06	-4.2354e-06	-4.84717e-06	-5.37263e-06	-5.80632e-06	-6.14338e-06	-6.3796e-06	-6.51141e-06	-6.53593e-06	-6.45096e-06	-6.25495e-06	-5.94705e-06	-5.5271e-06	-4.99559e-06	-4.35368e-06	-3.60318e-06	-2.74656e-06	-1.78688e-06	-7.27811e-07	4.26393e-07	1.67094e-06	3.00049e-06	4.40924e-06	5.89092e-06	7.4388e-06	9.0458e-06	1.07045e-05	1.2407e-05	1.41454e-05	1.59113e-05	1.76963e-05	1.94917e-05	2.12888e-05	2.30788e-05	2.48527e-05	2.66018e-05	2.83173e-05	2.99904e-05	3.16127e-05	3.31757e-05	3.46713e-05	3.60916e-05	3.74288e-05	3.86758e-05	3.98255e-05	4.08714e-05	4.18073e-05	4.26274e-05	4.33265e-05	4.38999e-05	4.43431e-05	4.46525e-05	4.48249e-05	4.48575e-05	4.47483e-05	4.44957e-05	4.40988e-05	4.35572e-05	4.28711e-05	4.20413e-05	4.10691e-05	3.99566e-05	3.8706e-05	3.73206e-05	3.58039e-05	3.41599e-05	3.23933e-05	3.05092e-05	2.85131e-05	2.6411e-05	2.42094e-05	2.19149e-05	1.95349e-05	1.70769e-05	1.45485e-05	1.1958e-05	9.31361e-06	6.62394e-06	3.8977e-06	1.14376e-06	-1.62889e-06	-4.41119e-06	-7.19403e-06	-9.96831e-06	-1.27249e-05	-1.54548e-05	-1.81491e-05	-2.07989e-05	-2.33956e-05	-2.59307e-05	-2.83959e-05	-3.07832e-05	-3.30849e-05	-3.52935e-05	-3.74019e-05	-3.94034e-05	-4.12915e-05	-4.30602e-05	-4.4704e-05	-4.62177e-05	-4.75966e-05	-4.88364e-05	-4.99334e-05	-5.08843e-05	-5.16863e-05	-5.23372e-05	-5.2835e-05	-5.31787e-05	-5.33673e-05	-5.34008e-05	-5.32793e-05	-5.30037e-05	-5.25751e-05	-5.19955e-05	-5.1267e-05	-5.03924e-05	-4.93749e-05	-4.82182e-05	-4.69263e-05	-4.55038e-05	-4.39555e-05	-4.22868e-05	-4.05033e-05	-3.86109e-05	-3.66161e-05	-3.45254e-05	-3.23457e-05	-3.00841e-05	-2.77479e-05	-2.53447e-05	-2.28823e-05	-2.03683e-05	-1.78109e-05	-1.52181e-05	-1.2598e-05	-9.95864e-06	-7.3083e-06	-4.65507e-06	-2.00704e-06	6.27785e-07	3.24149e-06	5.82629e-06	8.37455e-06	1.08788e-05	1.33318e-05	1.57265e-05	1.8056e-05	2.03139e-05	2.24938e-05	2.45899e-05	2.65964e-05	2.85081e-05	3.03199e-05	3.20273e-05	3.3626e-05	3.51122e-05	3.64824e-05	3.77335e-05	3.8863e-05	3.98685e-05	4.07483e-05	4.1501e-05	4.21256e-05	4.26215e-05	4.29886e-05	4.32271e-05	4.33379e-05	4.33219e-05	4.31808e-05	4.29162e-05

filtglass(:,1) = filtfilt(fkern, 1, glassclip(:,1));
filtglass(:,2) = filtfilt(fkern, 1, glassclip(:,2));
filtglass(1:10,:)

ans	1	2
1	-3.51718e-22	2.8002e-21
2	-6.28728e-08	-6.60062e-07
3	-1.28644e-07	-1.32039e-06
4	-2.00192e-07	-1.98126e-06
5	-2.80361e-07	-2.64291e-06
6	-3.71938e-07	-3.30556e-06
7	-4.77639e-07	-3.96942e-06
8	-6.00091e-07	-4.63464e-06
9	-7.4181e-07	-5.30133e-06
10	-9.05189e-07	-5.96957e-06

pow_filt = abs(fft(filtglass(:,1))/pnts);
pow_filt(1:10)

ans	1
1	2.93672e-06
2	2.93672e-06
3	2.93672e-06
4	2.93672e-06
5	2.93672e-06
6	2.93672e-06
7	2.93672e-06
8	2.93672e-06
9	2.93672e-06
10	2.93673e-06

figure(3), clf
subplot(311)
plot(timevec, glassclip)
xlabel('Time (s) ')

hold on
plot(timevec, filtglass)
hold off

subplot(312), cla
plot(hz, pow(1:length(hz)))
xlabel('Frequency (Hz)' ), ylabel('Amplitude')

subplot(313), cla
plot(hz, pow(1:length(hz)))
set(gca, 'xlim', [100 2000], 'ylim', [0 max(pow)])
xlabel('Frequency Range Limited (Hz) '), ylabel('Amplitude')

hold on
plot(hz, pow_filt(1:length(hz)), 'r')
hold off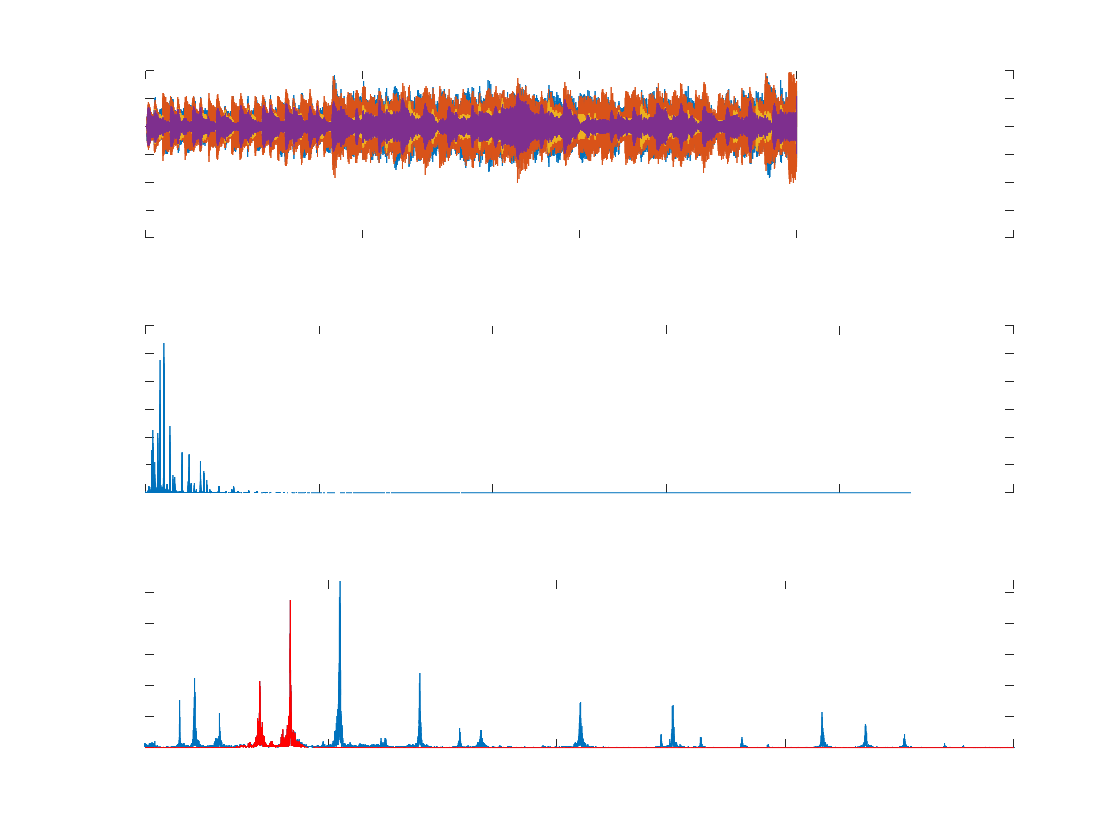

warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)
warning: opengl_renderer: invalid image size (expected MxNx3 or MxN)

Spectogram (Time Frequency Response)

• Time on x-axis
• Frequency on y-axis
• Color blob energy at that point

help specgram

'specgram' is a function from the file /home/rahuketu/.local/share/octave/api-v57/packages/signal-1.4.5/specgram.m

 -- Function File: specgram (X)
 -- Function File: specgram (X, N)
 -- Function File: specgram (X, N, FS)
 -- Function File: specgram (X, N, FS, WINDOW)
 -- Function File: specgram (X, N, FS, WINDOW, OVERLAP)
 -- Function File: [S, F, T] = specgram (...)

     Generate a spectrogram for the signal X.  The signal is chopped
     into overlapping segments of length N, and each segment is windowed
     and transformed into the frequency domain using the FFT. The
     default segment size is 256.  If FS is given, it specifies the
     sampling rate of the input signal.  The argument WINDOW specifies
     an alternate window to apply rather than the default of ‘hanning
     (N)’.  The argument OVERLAP specifies the number of samples overlap
     between successive segments of the input signal.  The default
     overlap is ‘length (WINDOW)/2’.

     If no output arguments are given, the spectrogram is displayed.
     Otherwise, S is the complex output of the FFT, one row per slice, F
     is the frequency indices corresponding to the rows of S, and T is
     the time indices corresponding to the columns of S.

     Example:
             x = chirp([0:0.001:2],0,2,500);  # freq. sweep from 0-500 over 2 sec.
             Fs=1000;                  # sampled every 0.001 sec so rate is 1 kHz
             step=ceil(20*Fs/1000);    # one spectral slice every 20 ms
             window=ceil(100*Fs/1000); # 100 ms data window
             specgram(x, 2^nextpow2(window), Fs, window, window-step);

             ## Speech spectrogram
             [x, Fs] = auload(file_in_loadpath("sample.wav")); # audio file
             step = fix(5*Fs/1000);     # one spectral slice every 5 ms
             window = fix(40*Fs/1000);  # 40 ms data window
             fftn = 2^nextpow2(window); # next highest power of 2
             [S, f, t] = specgram(x, fftn, Fs, window, window-step);
             S = abs(S(2:fftn*4000/Fs,:)); # magnitude in range 0<f<=4000 Hz.
             S = S/max(S(:));           # normalize magnitude so that max is 0 dB.
             S = max(S, 10^(-40/10));   # clip below -40 dB.
             S = min(S, 10^(-3/10));    # clip above -3 dB.
             imagesc (t, f, log(S));    # display in log scale
             set (gca, "ydir", "normal"); # put the 'y' direction in the correct direction

     The choice of window defines the time-frequency resolution.  In
     speech for example, a wide window shows more harmonic detail while
     a narrow window averages over the harmonic detail and shows more
     formant structure.  The shape of the window is not so critical so
     long as it goes gradually to zero on the ends.

     Step size (which is window length minus overlap) controls the
     horizontal scale of the spectrogram.  Decrease it to stretch, or
     increase it to compress.  Increasing step size will reduce time
     resolution, but decreasing it will not improve it much beyond the
     limits imposed by the window size (you do gain a little bit,
     depending on the shape of your window, as the peak of the window
     slides over peaks in the signal energy).  The range 1-5 msec is
     good for speech.

     FFT length controls the vertical scale.  Selecting an FFT length
     greater than the window length does not add any information to the
     spectrum, but it is a good way to interpolate between frequency
     points which can make for prettier spectrograms.

     After you have generated the spectral slices, there are a number of
     decisions for displaying them.  First the phase information is
     discarded and the energy normalized:

     S = abs(S); S = S/max(S(:));

     Then the dynamic range of the signal is chosen.  Since information
     in speech is well above the noise floor, it makes sense to
     eliminate any dynamic range at the bottom end.  This is done by
     taking the max of the magnitude and some minimum energy such as
     minE=-40dB. Similarly, there is not much information in the very
     top of the range, so clipping to a maximum energy such as maxE=-3dB
     makes sense:

     S = max(S, 10^(minE/10)); S = min(S, 10^(maxE/10));

     The frequency range of the FFT is from 0 to the Nyquist frequency
     of one half the sampling rate.  If the signal of interest is band
     limited, you do not need to display the entire frequency range.  In
     speech for example, most of the signal is below 4 kHz, so there is
     no reason to display up to the Nyquist frequency of 10 kHz for a 20
     kHz sampling rate.  In this case you will want to keep only the
     first 40% of the rows of the returned S and f.  More generally, to
     display the frequency range [minF, maxF], you could use the
     following row index:

     idx = (f >= minF & f <= maxF);

     Then there is the choice of colormap.  A brightness varying
     colormap such as copper or bone gives good shape to the ridges and
     valleys.  A hue varying colormap such as jet or hsv gives an
     indication of the steepness of the slopes.  The final spectrogram
     is displayed in log energy scale and by convention has low
     frequencies on the bottom of the image:

     imagesc(t, f, flipud(log(S(idx,:))));

Additional help for built-in functions and operators is
available in the online version of the manual.  Use the command
'doc <topic>' to search the manual index.

Help and information about Octave is also available on the WWW
at https://www.octave.org and via the help@octave.org
mailing list.

[powspect,frex,time] = specgram(glassclip(:,1),1000,srate,hann(round(srate/10)));

warning: specgram fft size adjusted to 4410
warning: called from
    specgram at line 152 column 5

figure(4), clf
subplot(511)
plot(timevec, glassclip)
xlabel('Time (s) ')

hold on
plot(timevec, filtglass)
hold off

subplot(512), cla
plot(hz, pow(1:length(hz)))
set(gca, 'xlim', [100 2000], 'ylim', [0 max(pow)])
xlabel('Frequency Range Limited (Hz) '), ylabel('Amplitude')

hold on
plot(hz, pow_filt(1:length(hz)), 'r')
hold off

subplot(5,1, 3:5), cla
specgram(glassclip(:,1),1000,srate,hann(round(srate/10)))
hold on
plot(timevec([1 1; end end]),frange([1 2; 1 2]),'k:','linew',2)
set(gca, 'ylim', [0 2000])
hold off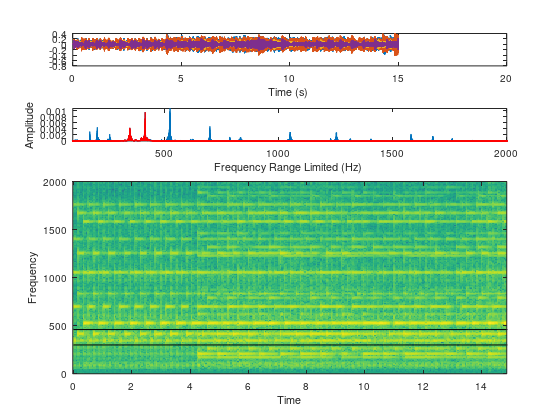

warning: specgram fft size adjusted to 4410
warning: called from
    specgram at line 152 column 5

warning: set: allowing linew to match line property linewidth
warning: called from
    __plt__>__plt2mm__ at line 295 column 15
    __plt__>__plt2__ at line 257 column 14
    __plt__ at line 114 column 16
    plot at line 235 column 10

warning: set: allowing linew to match line property linewidth
warning: called from
    __plt__>__plt2mm__ at line 295 column 15
    __plt__>__plt2__ at line 257 column 14
    __plt__ at line 114 column 16
    plot at line 235 column 10

Specgram works in gnuplot backend on octave environment but doesnot seem to work on notebook / plotly backend

whos

Variables visible from the current scope:

variables in scope: top scope

  Attr   Name           Size                     Bytes  Class
  ====   ====           ====                     =====  ===== 
         ans            1x1                          8  double
         channel        1x1                          8  double
         doc_file       1x79                        79  char
         filtglass 661500x2                   10584000  double
         fkern          1x2002                   16016  double
         frange         1x2                         16  double
         frex           1x2205                   17640  double
         glassclip 661500x2                   10584000  double
         hz             1x330751               2646008  double
         pkg_dir        1x64                        64  char
         pnts           1x1                          8  double
         pow       661500x1                    5292000  double
         pow_filt  661500x1                    5292000  double
  c      powspect    2205x298                 10513440  double
         srate          1x1                          8  double
         time           1x298                     2384  double
         timevec        1x661500               5292000  double

Total is 5622995 elements using 50239679 bytes